こんにちは、ゆるカピです。
あなたはこんなことに悩んでいませんか。

建築士試験の構造力学の問題が苦手

構造の参考書だけではよくわからなかった
この講座では、
- 計算の苦手意識を克服する
- 建築士試験の力学の問題を得点源にする
ことを目指すあなたを応援します。すべて無料で公開予定です。
第2回目は「力のモーメント」について解説していきます。
私は、大学院生時代構造系の研究室に所属していて、たくさんの力学を勉強する学生の質問に答えてきました。感覚として、だいたいこのあたりから苦手意識を持つ人が増えてくる印象を受けます。
今回の内容でよくある間違いや詰まるところは、
- モーメント荷重に距離をかけてしまう
- 断面一次モーメントがわからない
です。

よく間違える人は、特にこのあたりに注意してみてね。
力のモーメント

力のモーメントは、よく「てこの原理」で説明されます。
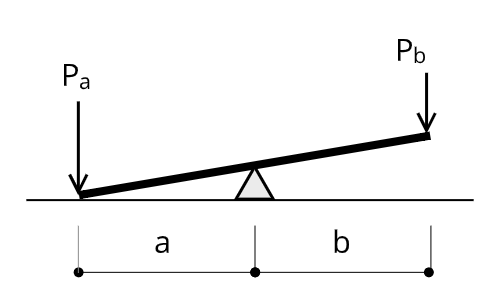
例えば、シーソーをイメージしてみるとわかりやすいでしょう。シーソーの端に力を作用させると、もう一方の端が持ち上がりますよね。
このようなてこに作用する力は、支点回りに回転させようとするとも言えます。
この時、
$$P_{a} : P_{b} = b : a$$
あるいは、
$$P_{a} a = P_{b} b$$
の関係が成り立ちます。これが力のモーメントです。単位は力に距離を掛けたものなので、kN・mやN・mなどと表現されます。
偶力のモーメント
偶力とは、同じ大きさで平行かつ反対方向の2つの力のことです。
第1回の力のつり合いでは、2つの力が、同じ力の作用線上にあれば、
$$A + B = 0$$
となり、力がつり合っているという話をしました。
では、それぞれ別の力の作用線を形成している、つまり、お互い平行の関係にある場合はどのようになるかというと、2つの力が作用する物体は回転します。
偶力とモーメントの関係
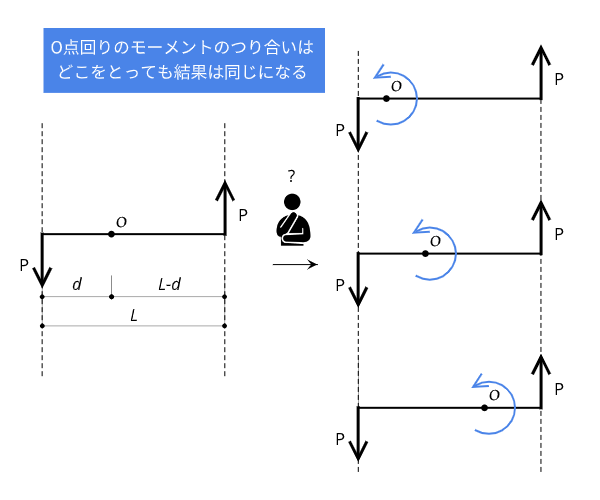
偶力を$P$として任意の点$O$の位置から作用しているとすると、偶力のモーメントの和$M$は次のようになります。
$$M = P ( L- d ) + P d = P L$$
つまり、偶力のモーメント$M$は支点をどこに置いても変わらないことがわかります。
上の式の関係から、偶力$P = M / L$とも表せます。
重心と図心、断面一次モーメント

重心という言葉の定義は知らなくても、ものの重心の位置は経験的に知っている人は多いと思います。
ものを持つ時、無意識的に重心の位置で持とうとしますよね。

力自慢で変わったところを持つ人はいるかもしれないけど•••。
レストランのウェイトレスが食事を運ぶイメージって、トレーの真ん中を持っていますよね。これは少ない力でものを運ぶことができるからです。もし、トレーの端だけを持って食事を運ぼうとすると、真ん中で持った時よりも力を入れて運ばないといけません。
てこの原理につながる話ですね。
重心から離れた分だけ、力のモーメントが大きくなるということです。
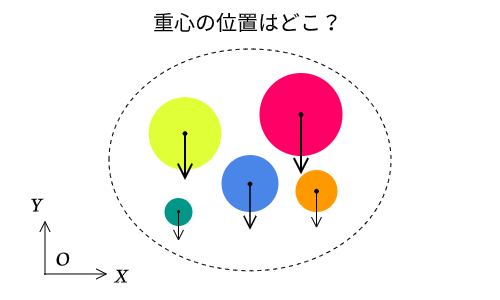
重心の計算公式
重心は計算では以下のように求められます。
$$x_{G} = \frac{\sum_{}^{}{x_{i}\cdot m_{i}}}{\sum_{}^{}{m_{i}}}$$
($m$は質量、$x$は原点$O$からある物体までの距離とする)
小難しい数式が出てきました。
とりあえずは、重量にそれぞれの距離$x$を掛けたものの合計を全部の重量で割ったら(平均化したら)、重心が求められるという感じで大丈夫です。
図心
重心は知ってるけど、図心って聞いたことないという人は世の中にはたくさんいると思います。
でもここで、また新しい用語か、と身構える必要はありません。
重心は実際のものに作用する力の中心点なのに対して、図心は平面系(厚みのないぺらぺらの紙をイメージしてください)で考えた時の作用する力の中心点を表しています。
なので、基本的な考えは重心と同じです。
断面一次モーメント
そもそも断面一次モーメントがよくわからない、という話をよく聞きます。モーメントという名前がついているのに、単位系が$m^3$のように長さの3乗になっていたり、断面二次モーメントとの関係性だったりと謎なことが多いためです。
断面一次モーメントは英語でgeometrical moment of areaといいます。計算式でも、
$$S_{y} = \int_{A}^{}xdA$$
となっているように、微小面積$dA$に$y$軸からの距離$x$を掛けているので、面積を質量(密度)として置き換えてみると、「面積モーメント」と考えても良さそうです。
ここで、面積を質量として考えるというのがポイントです。
そうです、質量とその距離の積を全体の質量で割ったら重心が出てきましたよね。これと同じ考えで、なんと断面一次モーメントから図心が求められるのです。
なんだか、わかったようなわからないような•••、と思うかもしれませんが、ほとんどの人はそれで大丈夫です。
断面一次モーメントそのものは単に計算過程で出てきたものなので、あまり深く考える必要はありません。建築士試験だけの話で言えば、
$$図心x_{G} = \frac{ある断面積A \times y軸からの距離}{全断面積}$$
を覚えておけば十分です。
ここでひとつ注意点があります。
図心の$x$座標の値を求める時は$y$軸からの距離、$y$座標の値を求める時は$x$軸からの距離というように、$x$と$y$は対(つい)の関係になっています。
問題を解く時は$x$と$y$をごっちゃにしないようにしましょう。
具体的な計算の解き方を知りたい場合は、こちらの記事も参考にどうぞ。
まとめ
お疲れ様でした。
今回はそこそこ難しい内容だったかと思います。ぜひ、試験勉強の参考にしてみてください。
次回は「引張、圧縮」について解説していきます。
それでは、また。




































コメント