こんにちは、ゆるカピ(@yurucapi_san)です。
パソコン作業をしていたら、ふとマグカップに手が当たって飲みかけのコーヒーをブチまけた、っていう経験はありませんか。
デスクワークをしている人なら一度や二度どころの話ではないのではないでしょうか。
私もたまにやらかします。普段は気をつけてマグカップとマウス・キーボードを離しているんですが、ちょっと油断したタイミングでやってしまいます...。
でも、軽く手が触れた程度なら中身はこぼれませんよね。いわゆるセーフってやつです。
今回は、この現象を転倒と滑動という力学の観点から解説したいと思います。
マグカップが倒れる仕組み
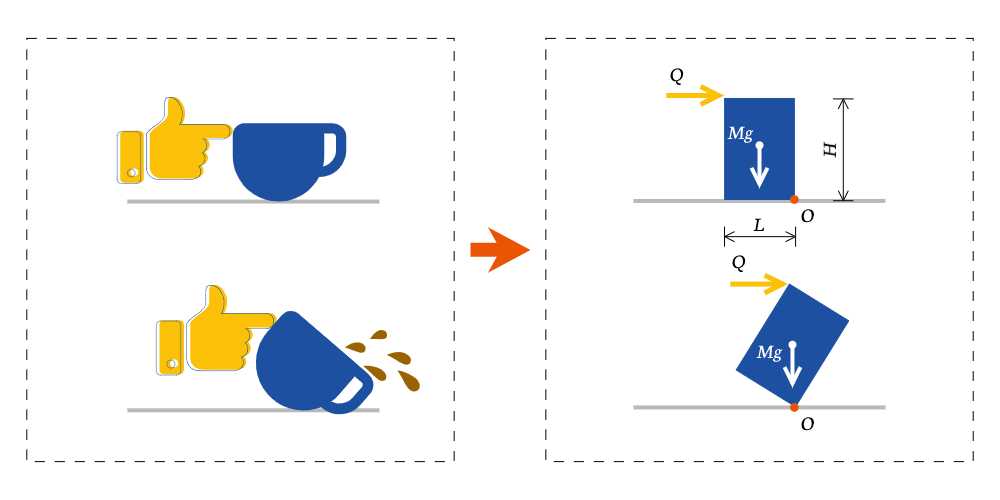
マグカップの転倒のモデルは、左から押す力$Q$が作用した時の物体の転倒に置き換えて考えることができます。
この時、マグカップ本体と中身を合わせた重量$Mg$が下向きに作用しています。水平力$Q$を押していくと、点$O$を回転中心として回転しながら転倒します。水平力$Q$と重量$Mg$の2つの力によるモーメントのつり合いを考えてみましょう。
物体の幅$L$と高さ$H$とすると、
$$Q \times H - Mg \times \frac{L}{2} = 0 \Leftrightarrow Q = \frac{L}{2H}Mg$$
となります。$L = H$の場合は重量の半分の力が作用すると転倒し始めるということがわかります。$QH$を転倒モーメント、$MgL/2$を安定モーメントと呼ぶこともあります。
ちなみに、倒れないマグカップというのがあるそうです。デスクのそばに飲み物を置いておきたいけどこぼしたくない人には救いの手になるかも...。なんと、あの「月曜から夜ふかし」でも取り上げられていたらしいです。
気になる人はぜひお試しあれ!
マグカップが滑るのはどういう時?
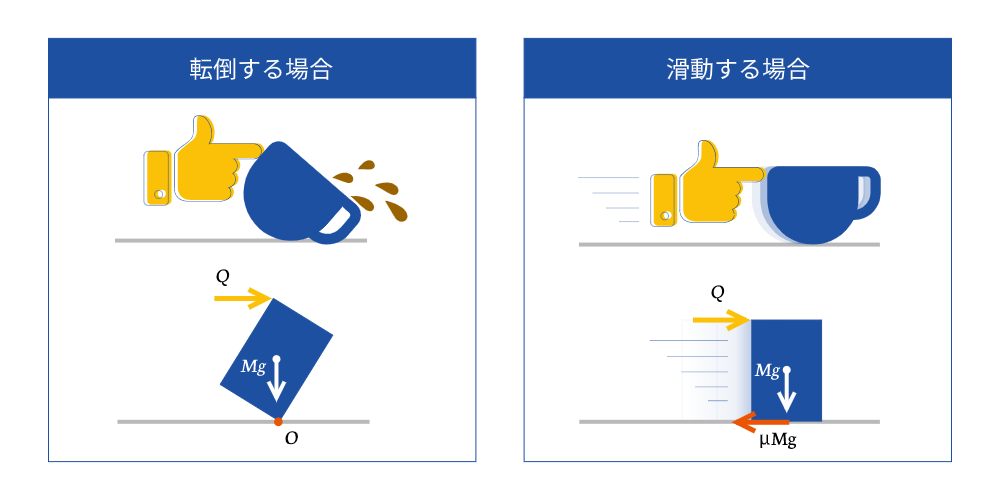
マグカップの転倒は、実は点$O$で滑らない前提の話です。では、どんな時滑るのでしょうか。
最大摩擦力の公式に先ほどの力を当てはめてみると$Q = \mu Mg$となります。滑らないようにするには、摩擦係数$\mu$ができるだけ大きい材料を選ぶか、本体と中身の重量を重くするかしないといけません。
建築材料の摩擦係数
一般的に材料ごとの摩擦係数は次のようになっています(設計便覧より参照)。この数値はあくまで一般的なものなので、実際には実験で求めるのがいいと思います。
| 摩擦面の組み合わせ | 摩擦係数$\mu$ |
|---|---|
| 石-金属 | 0.3~0.4 |
| 石-土 | 0.5(乾)~0.3(湿) |
| 土-土 | 0.25~1.0 |
| 木-木 | 0.5(乾)~0.2(湿) |
| 木-石 | 0.4 |
| 木-金属 | 0.6(乾)~0.2(湿) |
| ゴム-ゴム | 0.5 |
鋼材の摩擦係数
鋼材の摩擦係数では以下の実験値を使う場合が多いです。高力ボルトの計算などで使います。
| 鋼材の種類 | 表面処理方法 | 摩擦係数 |
|---|---|---|
| 構造用鋼材 | 浮き錆を除去した赤錆面 ブラスト処理面(50$\mu mRy$以上) 無機ジンクリッチ塗料塗装面 (塗膜厚45~75$\mu mRy$程度) | 0.45 |
| 構造用鋼材 | 第3種ケレン処理後の黒皮面 | 0.23 |
| 溶融亜鉛めっき構造用鋼材 | ブラスト処理面(50$\mu mRy$以上) | 0.40 |
| 板厚6㎜未満の鋼材 | 上記のいずれかの処理 | 0.23 |
表面処理方法たくさんあってよくわからないと思いますが、大抵は最大静止摩擦係数$\mu = 0.45$が標準ということで大丈夫でしょう。
設計ではどんな時に使う?

設計実務では以下の場面で使います。
- ブロック塀の計算
- 堤防、擁壁のの計算
- 案内板の基礎の計算
- 塔状比4以上の建築物の計算
2018年に発生した大阪府北部地震では、学校に設置されていたブロック塀が倒壊し、登校中だった小学4年生の女児が亡くなっています。現在はさまざまな対策が行われて、安全性の確保や危険なブロック塀の撤去が進んでいます。
このような被害をなくしていくためにも、安全性に配慮した設計を心がけたいですね。
転倒、滑動しないようにするには...
転倒、滑動に対して最も効果的なのは、重量を増やすことです。とは言っても建築物の重量は増やせないので、基礎のコンクリートを増し打ちして対応するのが一般的です。べた基礎を採用するのも対処法のうちのひとつです。
また、建築物の規模によっては引き抜き抵抗のための杭を打設する場合も考えられます。
いずれにしても、基礎と本体の建築物との間を鉄筋やアンカーなどで十分に固定しないと、本体だけ転倒してしまうということになってしまいます。
塔状比4以上の建築物のルール
塔状比4以上の建築物については、保有水平耐力計算をすることが建築基準法で義務付けられています。例えば、建築物の高さが20m、間口が5mだとしたらちょうど塔状比が4になります。これが、建築物の高さが15mだったら塔状比は3なので保有水平耐力計算は不要です。
間口が狭くて高さがある細長い建築物は、地震や台風などの水平力がかかった時に転倒するリスクが非常に高いです。なので、塔状比が4以上の建築物については、詳細な計算をして安全性を確認することが求められているわけです。
まとめ
転倒や滑動はとても身近な現象ですが、いざ力学の問題になるとあれ?って慌てませんか。物体の転倒や塔状比の問題は最近の建築士試験で出題されています。力学の仕組みとして理解しておけば、問題を解くのも簡単になるはずです。ぜひ、試験対策に役立ててみてください。
こんな感じで構造力学の基礎シリーズも第19回を迎えました。まだ第1回目を読んでいない人はこちらからどうぞ。それでは、また。


































コメント