こんにちは、ゆるカピ(@yurucapi_san)です。
あなたは、物を思いっきり引っ張ったり曲げたりする時、変形したまま元に戻らないという経験はありますか。例えば、輪ゴムを勢いよく引っ張ったり、スプーンを強い力で折り曲げたり、といった感じの経験です。
力を加えて生じた変形が一度力を抜いても元に戻らなくなる物体の性質のことを、塑性といいます。今回は塑性について解説していきたいと思います。

構造設計では重要な話だから、弾塑性についてしっかり理解しよう。
弾塑性のメカニズム
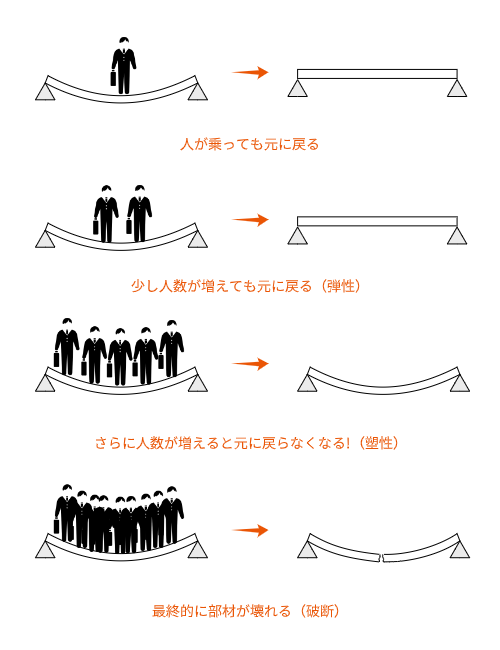
力が作用して変形しても、力を取り除くと元に戻る現象が弾性です。この時、力と変形が比例関係にあり、フックの法則が成り立ちます。
しかし、ある一定以上の力が作用して変形すると、力を取り除いても元に戻らなくなる状態になります。これが塑性です。
弾性状態から塑性状態に切り替わる瞬間のことを降伏といいます。部材が力負けしちゃうってことです。部材が降伏した後は力と変形の関係が一定ではなくなるため、フックの法則が成り立ちません。
塑性変形が進むとやがて部材は破断して壊れてしまいます。このように、力をかけていくと弾性→塑性→破断のプロセスをたどる材料の性質を弾塑性と呼んでいます。
応力-ひずみ曲線図から考える
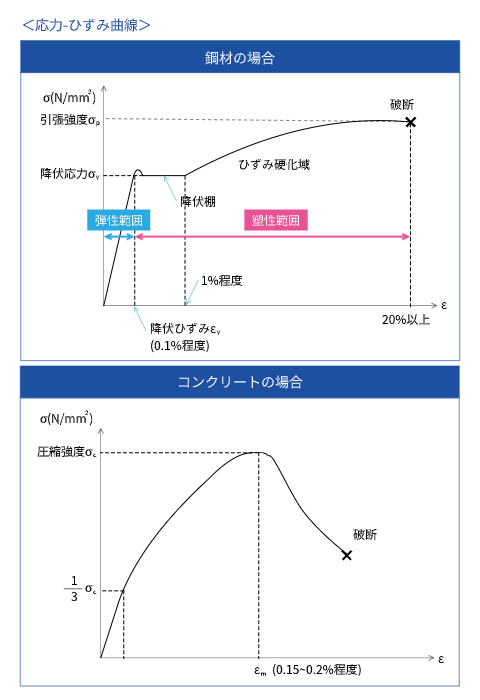
弾塑性の性質をもつ材料は図のような応力-ひずみ曲線図を描きます。これは鋼材やコンクリートなどの材料によって描き方が違います。この図は弾塑性の性質を視覚的に知るうえで役に立つと思うので、この図の形状を覚えておくといいでしょう。
塑性変形=危険ではない
塑性というと英語でplasticと表現するのでプラスチック製品のようにボロボロになるイメージを想像してしまいますが、鋼材やコンクリートなどの建築材料の塑性変形は決して危険な状態ではありません。
塑性は脆性とは違います。脆性とは、例えばガラスのように、力が加わると変形するまでもなく簡単に割れたり壊れたりする性質のことです。建築の構造駆体に使う材料がちょっとの力で簡単に壊れたら大変ですよね。
塑性よる破壊はある程度変形が進んでから起こります。その変形が進むまでは部材が壊れて建築物が崩壊することはありません。

急激にひび割れが進行して部材が壊れるせん断破壊も脆性破壊の一種だよ。構造設計では耐震壁を除いて、せん断破壊させないようにするのが原則だよ。
塑性変形で期待できること
これは、部材が降伏してから破断するまで余裕があると見ることができます。部材が完全に壊れるまでは変形だけ進むので、変形した分のエネルギー吸収を期待することができます。
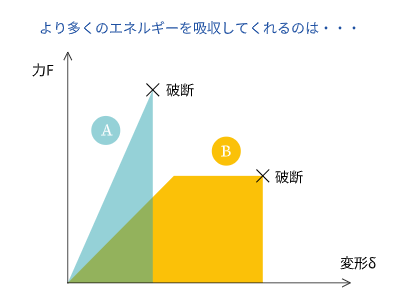
例えば、図のように力をかけていった時に、Aの場合とBの場合、どちらがより多くのエネルギーを吸収してくれるでしょうか?
答えは、Aより面積の大きいBです。Bのほうは塑性化してから破断するまでの変形によるエネルギー分も吸収しているからです。
降伏比によって部材の余裕度が変わる
この特性を期待して降伏比を下げている鋼材のことを低降伏点鋼といいます。降伏比は降伏応力を最大強度で割ったもので、降伏してから破断するまでの余裕度を図る指標です。
$$降伏比 = \frac{降伏強度}{最大強度}$$
鋼材の例えばSN400材の場合、降伏応力$\sigma_y = 235 N/mm^2$、最大強度$400 N/mm^2$なので、降伏比は58.8%と6割程度の値になります。
降伏比が小さい(降伏応力が小さく、最大強度が大きい)と、より多くのエネルギー吸収が期待できます。
建築士試験の勉強をしていると、降伏比の分母分子、どっちが上で下なのかわからなくなりますよね。こういう比を表す用語は分子に来るものがそのまま用語になっている場合がほとんどだと思います。幅厚比とかもそうです。規則性を覚えておきましょう。
全塑性モーメント
柱や梁などの比較的長い部材は、大きな力がかかって変形が進むと塑性化します。曲げ変形が進んで塑性化した時のモーメントはどのようになっているでしょうか。ここでは長方形断面のモデルについて考えたいと思います。
全塑性モーメントのメカニズム
弾性状態の曲げ応力と曲げモーメントの関係は、$M = \sigma_b Z$でした。曲げモーメントが大きくなると曲げ応力$\sigma_b$も大きくなり、断面の上下の最外端が降伏応力$\sigma_y$に達します。この時の曲げモーメントのことを降伏モーメント$M_y$といいます。
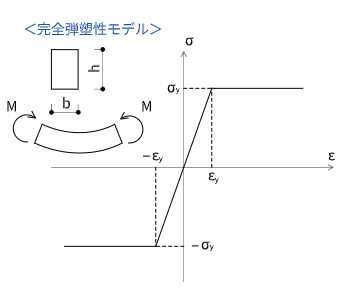
塑性変形では、応力が降伏強度$\sigma_y$で頭打ちになってひずみ(変形)だけが進みます。応力が降伏応力を超えないということがポイントです。
鋼材の場合、厳密には降伏応力より破断強度(引張強度)のほうが大きいのですが、応力の変化はひずみの変化に比べて小さいため、構造力学では応力が降伏応力を超えない完全弾塑性モデルで考えることが多いです。
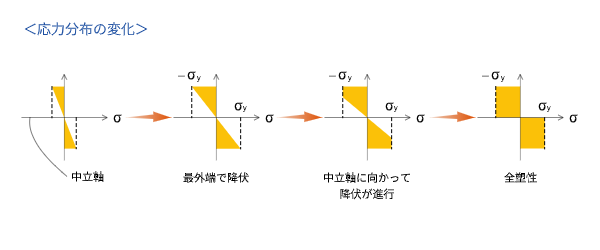
変形が進むにつれて、断面の上下の最外端から中立軸に向かって塑性化していきます。すると、応力分布は三角形分布から台形分布に変化します。さらに、塑性化の範囲が中立軸に達して部材全体が塑性化した時、応力分布は最終的に長方形分布になります。
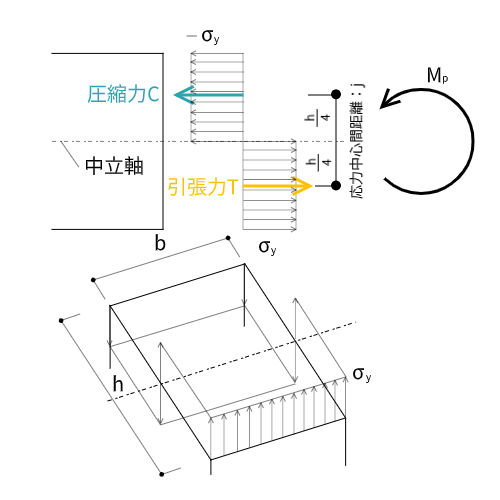
この時の部材を全塑性といい、生じている曲げモーメントのことを全塑性モーメントといいます。式で表すと、
$$M_p = \sigma_y Z_p$$
です。$Z_p$は塑性断面係数を表しています。
長方形断面の塑性断面係数の求め方
長方形断面の塑性断面係数$Z_p$は断面係数$Z$と同じやり方で求められます。

あれ、塑性状態ってフックの法則が成り立たないんじゃないの?どうして同じやり方で求められるの?

塑性変形でも、瞬間ごとの力のつり合いは成立しているよ。あくまで応力とひずみの関係が一定の変化じゃなくなるだけだよ。
全塑性の状態は部材が壊れる瞬間の状態なので、この時の応力のつり合いは成立しています。なので、弾性状態と同じように計算すれば大丈夫です。長方形分布なので計算自体は断面係数より簡単に求められると思います。
求めると、
$$Z_p = \frac{bh^2}{4}$$
という答えが出てきます。つまり、断面係数$Z$は塑性断面係数$Z_p$の2/3であることがわかります。降伏モーメント$M_y = \sigma_y Z$なので、
$$\frac{M_y}{M_p} = \frac{\sigma_y Z}{\sigma_y Z_p} = \frac{Z}{Z_p} = \frac{(2/3) Z_p}{Z_p} = \frac{2}{3}$$
となり、降伏比と同じく、降伏モーメントと全塑性モーメントの比も2/3(6割程度)の値になることがわかります。許容応力度設計で、短期許容応力度を材料強度の2/3とするのはこのあたりが関係しています。
まとめ
お疲れ様でした。
今回は塑性について解説をしました。弾塑性変形のイメージはつかめましたか。
塑性変形の理解は、建築物の壊れ方を知る第一歩です。許容応力度設計や保有水平耐力計算などの構造計算は弾塑性の考え方がベースになっているので、何度も復習して覚えておきましょう。
以下、関連記事です。曲げモーメントの基本や断面係数についてはこちらの記事も参考にしてみてください。それでは、また。


































コメント