こんにちは、ゆるカピです。
今回のテーマは「ラーメン構造」です。

ラーメンかあ〜最近食べてないな。ひさびさに食いたいな。
ラーメンは、食べるとカロリーがあって太るから毎回後悔するんですが、時間が空くとまた食べたくなるんですよね〜。ほんと、中毒性があります。
ちなみに、私の好みは塩ラーメン派です。年を重ねると、二郎系のこってり豚骨ラーメンは正直キツいですね。
•••というお決まりのラーメントークはさておき、構造力学のラーメン構造についてのお話をします。ラーメン構造の計算は結構つまずきやすい内容です。できる限り詳しく解説しようと思うので、今回の基本編と次回の演習編の2パートに分けることにしました。
それでは、早速始めます。
どんな構造?

梁と柱で構成される四角形状の骨組のことをラーメン構造といいます。
ラーメンというと食べ物のラーメンを思い浮かべますが、縁や枠などのことをドイツ語でラーメン(Rahmen)というそうです。ほかにも、せん断力を表す符号$Q$は、ドイツ語の横力(Quelkraft)から由来しています。
日本は昔ドイツからいろいろ建築技術を学んでたんだなあと感じさせる話ですね。
ラーメン構造の特徴
世の中にある鉄筋コンクリート造や鉄骨造の建物はだいたいがラーメン構造です。まずはその特徴について確認してみましょう。
- 空間の自由度が高い
- 施工が比較的容易
- 構造計画がわかりやすい
- 部材断面がほかと比べて大きめ
- 地震時に変形しやすい
- 構造のダイナミックさに欠ける
メリット
まずは巨匠ル・コルビュジエが提唱した「近代建築の五原則(Wikipedia)」のうちのひとつである自由な平面を体現したような構造ということです。空間の自由度が高まったおかげで、私たちはさまざまな施設計画を構造の制約を最小限に留めて自由に決めることができています。
さらに、施工もほかの架構形式と比べると容易で、コストメリットも大きいです。構造に関してみても、構造計画がシンプルでわかりやすいものにすることができるというのも最大の特徴です。
デメリット
一方で、ブレース構造や壁構造と比べて、部材の断面が大きくなりやすいというのは大きなデメリットになります。例えば、マンションなどで壁式鉄筋コンクリート造の架構形式が採用される理由として、室内に梁形や柱形を見せたくないというものがあります。
ワンルームのマンションに住んでいると、柱の出っこみが結構邪魔だなと感じませんか?
2つ目の変形しやすさについては、耐震性の観点では一概にデメリットとは言い切れません。しかし、鉄筋コンクリート造の場合、大地震が来た時に変形が大きくなるせいで、あとでひび割れの補修の手間がかかるという問題もあります。
3つ目については、構造で魅せたいと思っている人にとってはダイナミックさに欠けるので人気はないのかな、ということでデメリットに挙げました。
デメリット以上にメリットの恩恵が大きい
結論、世の中で圧倒的にラーメン構造の建物が多いのは、メリットの恩恵が大きいからでしょう。これは設計実務をしていて、特に実感することです。
最初はダイナミックな架構形式の提案に乗り気なクライアントも、いざ算盤を弾いてみるとラーメン構造でできないか、という話になります。
その話は抜きにしても、私自身、ラーメン構造はシンプルでわかりやすいので一番好きな架構形式ではあります。とりあえず、ラーメン構造にしておけば成立するだろうという安牌を狙えるのも設計者にとってのメリットと捉えています。
静定、不静定ラーメン構造
ラーメン構造は、静定ラーメンと不静定ラーメンに分けることができます。力学の話で言うと、つり合い式だけで問題が解けるかどうかという違いがあります。
静定、不静定について詳しくは第11回の記事で取りあげているのでこちらもご確認ください。
不静定ラーメン構造はつり合い式だけでは解けないため、解くためにはさらに別の条件式が必要になります。その条件式を使って手計算でも頑張れば解けるのですが、今は設計実務では解析ソフトで計算するのが一般的になっています。
だから、もう手計算で解かなくていいんだというわけにはいかないのが現実です。建築士試験レベルでも、静定ラーメン構造はよく出題されます。
なので、この基礎講座では静定ラーメン構造の問題の解き方について詳しく解説していきます。
部材と節点の関係

解き方の手順の話に入る前に、部材と節点について触れておきたいと思います。
構造力学では、私たちが柱や梁と考えているものを部材、部材と部材をつなぐ継ぎ目のことを節点と呼んでいます。部材は外力が作用すると応力が生じて変形しますが、節点そのものは伸び縮みなどの変形をしません。ピン接合の場合は部材に合わせて形状を保ったまま回転し、ラーメン構造の柱と梁の剛節部分の場合は部材に合わせて直角の形状を保ったまま移動するだけです。
また、柱と梁の剛節部分は応力をそのまま伝えるので、梁端部の曲げモーメントは大きさそのままで柱頭の曲げモーメントになります。
この考え方は、後で曲げモーメント図を描く時に役に立つので覚えておいてください。
解き方の手順を理解しよう

静定ラーメン構造の問題の解き方の手順は、基本的に単純梁の断面力の計算と同じです。
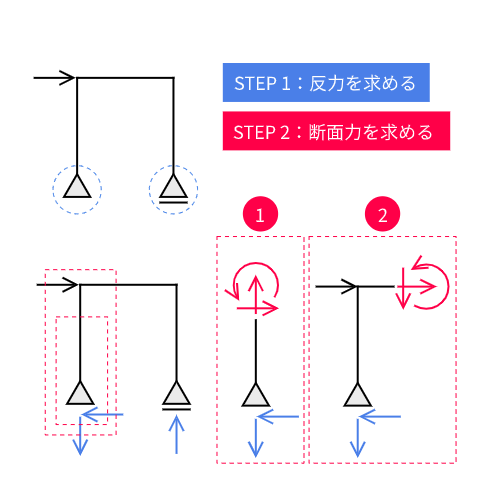
- STEP 1支点反力を求める
つり合い式を立てて支点反力を求める。
- $\Sigma H = 0$
- $\Sigma V = 0$
- $\Sigma M = 0$
求めた支点反力を図に書き込む。
- STEP 2各部材の断面力を求める
自由体図を描いてつり合い式を立てる。
- $\Sigma N = 0$
- $\Sigma Q = 0$
- $\Sigma M = 0$
つり合い式から断面力を求める。
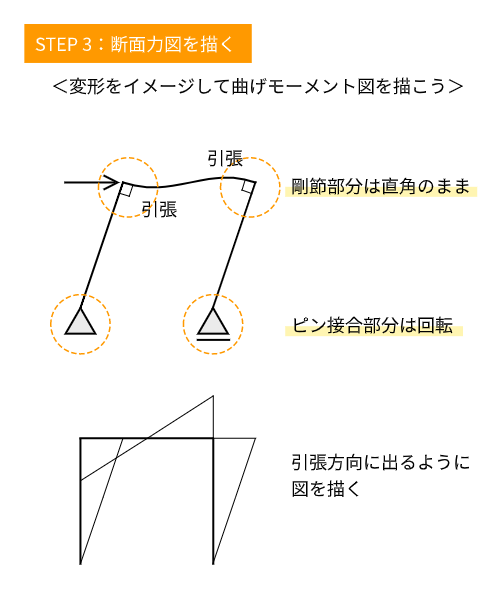
- STEP 3断面力図を描く
図の描き方のルールに注意して断面力図を描く。
ポイント①自由体図は部材軸を基準にする
柱が縦長、梁が横長なので、断面力の向きのルールを理解していないと大抵の場合、間違えます。理解があやふやな人は過去記事を参照してみてください。
自由体図で描く断面力の向きは、
- 軸力$N$は部材の長さ方向と同じ向き
- せん断力$Q$は部材軸に直角の向き
- 曲げモーメント$M$はせん断力に合わせるかたちで決める
とします。
梁部材を基準にしているので、柱部材を考える時は梁部材を90°回転させて考えればOKです。
ポイント②変形をイメージして曲げモーメント図を描く
曲げモーメント図を描く時は、変形をイメージして描くといいでしょう。ラーメン構造の場合は、門形の内側を正(プラス)、外側を負(マイナス)とするように描きます。
たぶん、これだけ読んでもなんのこっちゃ、となると思います。ラーメン構造の変形ってなかなかイメージがつかみづらいですから。
この時の助けになるのが、先ほど説明した部材と節点の関係です。柱と梁の剛節部分は90°形状を保ったまま部材が変形するので、描いていくうちに傾向がつかめるようになります。描いてみて正解のパターンを何回も見ての繰り返しをしていくうちになんとなく覚えられると思います。
まとめ
お疲れ様でした。
今回は、ラーメン構造の特徴と構造力学での問題の解き方について解説しました。そうは言っても、実際に手を動かさないとなかなか理解できないと思います。次回は解き方の手順を踏まえて、具体的にどう計算したらいいか、詳しく解説していきます。
それでは、また。




































コメント