こんにちは、ゆるカピです。
今回は「断面諸量」について解説します。
断面諸量というのは、断面一次モーメントや断面二次モーメントなどをまとめた総称のことです。
断面諸量そのものは上に挙げたもの以外にもいくつかありますが、今回は建築士試験にも直結する、断面一次モーメント、断面二次モーメント、断面係数の代表3種をご紹介します。
- 断面一次モーメントと断面二次モーメントの違い
- 断面二次モーメントと断面係数との関係
- 問題の解き方を例題で解説
それでは早速始めていきます。
断面一次モーメント

断面一次モーメントは別名面積モーメントとも言われていて、断面積に距離を掛けたものを合計すれば求められます。複数のモーメントの足し算みたいなものです。
距離の算定の元になる座標の原点は自分で設定することができます。どこでもいいのですが、大抵は図の左下に設定すると思います。
求めた断面一次モーメントを全断面積で割れば、図心を求めることができます。
計算例:H形断面の図心を求めよう
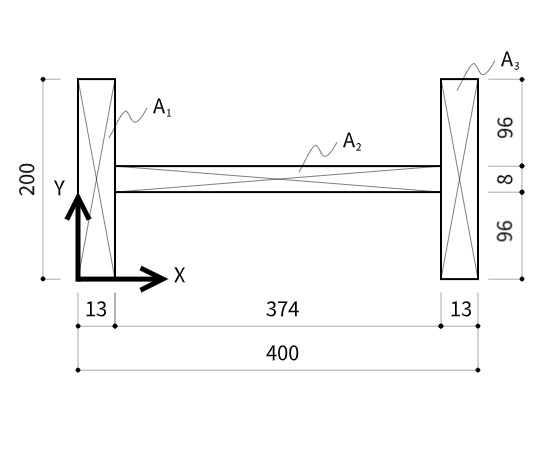
H形断面を例に、断面一次モーメントと図心を求めてみましょう。上下左右対照なので、おそらく図心の位置は計算しなくてもわかると思います。計算の流れを知って、求め方が間違っているかどうかの確認に使ってみてください。
断面一次モーメント$S_X$、$S_Y$を求める
左端からそれぞれの長方形の断面積を$A_1$、$A_2$、$A_3$とすると、
$$A_1 = A_3 = 13 \times 200 = 2,600 mm^2, A_2 = 374 \times 8 = 2,992 mm^2$$
なので、断面一次モーメントは、
$$S_Y = 2,600 \times 6.5 + 2,992 \times 200 + 2,600 \times 393.5 = 1,638,400 mm^3$$
$$S_X = 2,600 \times 100 + 2,992 \times 100 + 2,600 \times 100 = 819,200 mm^3$$
となります。
図心を求める
図心は、断面一次モーメントを全断面積$A_全$で割ると出てきます。
$$x_G = \frac{S_Y}{A_全} = \frac{1,638,400}{8,192} = 200 mm$$
$$y_G = \frac{S_X}{A_全} = \frac{810,200}{8,192} = 100 mm$$
断面二次モーメント
断面二次モーメントは、曲げモーメントとひずみの関係式を解いている過程で出てきた副産物で、曲げに対する固さ・変形しにくさの度合いを表す曲げ剛性$EI$に使われています。これについては別記事で解説しています。
つまり、曲げに抵抗できる固さを持たせるためには、材料を固いものにするか(ヤング係数$E$を上げる)、大きな断面にするか(断面二次モーメント$I$を大きくする)の組み合わせしかありません。
さらに、建築に使える材料は限られていて、ヤング係数を上げるのは現実的ではありません。例えばコンクリート強度をあげればヤング係数は若干上がりますが、その影響は微々たるものです。
このため、断面二次モーメントは設計するうえで重要な指標となります。
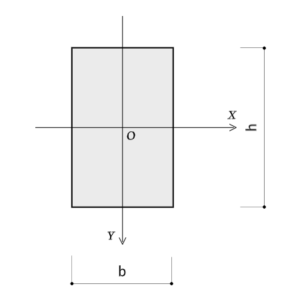
長方形断面の断面二次モーメント
長方形断面の断面二次モーメントはシンプルで汎用性が高いので、絶対に覚えておきましょう。
断面二次モーメントの公式は、その断面の図心が考える軸の上にないと使えないことに注意が必要です。これについては後ほど解説します。
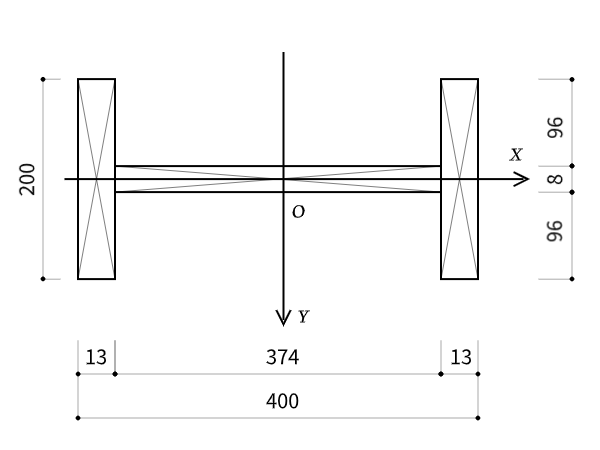
計算例:H形断面の断面二次モーメントを求めよう
早速、H形断面の場合を例に、断面二次モーメントを求めましょう。断面二次モーメントは定義どおりなら、積分を使って解かないといけないのですが、長方形断面の場合の公式を知っていれば、その組み合わせで比較的簡単に解くことができます。
$X$軸回りの断面二次モーメント$I_X$を求める
断面二次モーメント$I_X$は、3つの長方形断面の断面二次モーメントの足し算で計算できます。
$$I_X = \frac{13 \times 200^3}{12} + \frac{374 \times 8^3}{12} + \frac{13 \times 200^3}{12}$$
$$= 17,349,290.6 mm^4 \fallingdotseq 1,735 cm^4$$
$Y$軸回りの断面二次モーメント$I_Y$を求める
断面二次モーメント$I_Y$は、大きな長方形断面の断面二次モーメントから小さな長方形断面の断面二次モーメント2つを引いて求めます。
$$I_Y = \frac{200 \times 400^3}{12} - 2 \times \frac{96 \times 374^3}{12}$$
$$= 229,648,682.7 mm^4 \fallingdotseq 22,965 cm^4$$
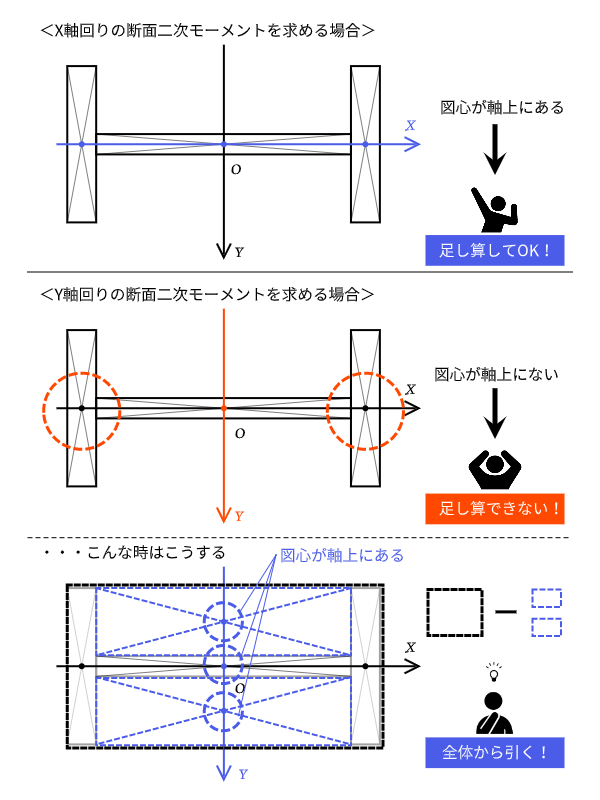
断面一次モーメントと断面二次モーメントの計算の違い

どちらも似たような名称で、断面積と距離を使って求めますが、両者を同じように計算すると間違いをしてしまいます。
先ほどのH形断面の例では、$I_X$では長方形断面の公式の足し算で求め、$I_Y$では全体から部分を引くという方法で求めていました。$I_Y$も足し算で求めてしまうと、違った答えが出てきて不正解になります。
足し算で解くか、全体から引く方法で解くかを決めるポイントは、それぞれの長方形断面の図心が考える軸の上に載っているかどうかです。
H形断面の場合、$I_Y$の時に引く長方形断面は軸の上に載っていますが、足し算で考えると両端の断面が軸から外れています。外れた状態でも補正の計算はできますが、面倒なうえに補正をかけなくても計算できる方法があるので、素直に足し算、引き算の両方のやり方を覚えたほうがいいでしょう。
一方、断面一次モーメントは、軸の上に載っているかどうかは気にする必要はありません。座標軸の中心は自分で設定でき、すべて足し算で計算できます。
断面係数
梁の場合、曲げ応力の最大値は断面の上下端になります。設計実務では部材の断面は最大応力で決まるので、最大応力がサクッとわかる指標があると便利です。
そこで登場するのが、断面係数$Z$です。
断面係数は、部材の断面二次モーメントを断面の中心から上端または下端までの距離$y$で割って求めます。
$$Z = \frac{I}{y}$$
曲げモーメントの式に代入すると、
$$M = \sigma_b Z$$
となります。
長方形断面の断面係数
長方形断面の場合、
$$I = \frac{bh^3}{12}$$
なので、
$$Z = \frac{\frac{bh^3}{12}}{\frac{h}{2}} = \frac{bh^2}{6}$$
となります。この式はよく使うので覚えておいたほうがいいでしょう。
曲げモーメントと断面係数の関係
$M = \sigma_b Z$を別のアプローチから求めてみましょう。
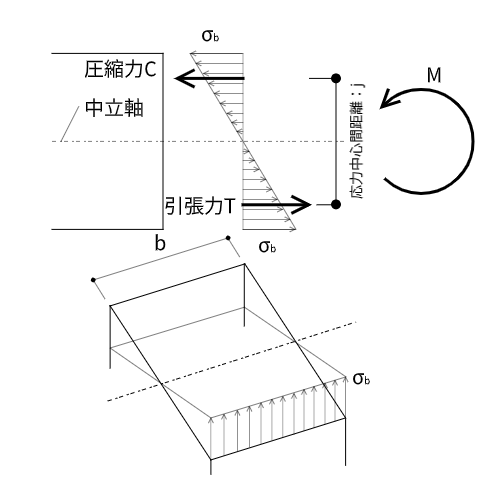
曲げモーメントは引張応力と圧縮応力の組み合わせでできたものなので、以下の式が成り立ちます。
- 引張力と圧縮力の偶力によるつり合い
$$T = C$$
- 曲げモーメント$M$について
$$M = T \times j$$
$$j = h - 2 \times (\frac{1}{3} \times \frac{h}{2}) = \frac{2}{3} h$$
$j$のことを応力中心間距離(レバーアーム)といいます。
- 引張力$T$について
$$T = \frac{1}{2} \times \frac{h}{2} \times \sigma_b \times b = \frac{bh}{4} \sigma_b$$
これらの式を連立して解くと、
$$M = \frac{bh}{4} \sigma_b \times \frac{2}{3} h = \frac{bh^2}{6} \sigma_b = \sigma_b Z$$
となり、断面二次モーメントを使わずに曲げモーメントと曲げ応力の関係式を求めることができました。
基本さえおさえておけば、この考え方はほかの断面でも応用できます。塑性曲げの問題でも使える方法なので、求め方を覚えておきましょう。
まとめ
お疲れ様でした。
今回の特に、断面二次モーメントの計算には慣れが必要です。基本となる長方形断面の公式を覚えて、たくさんの問題にチャレンジしてみてください。
それでは、また。




































コメント