こんにちは、ゆるカピです。
今回のテーマは「支点、反力」です。
支点と反力についてはこれまでも何度か登場してきましたが、今回は例題を交えてより詳しい解説をお届けします。

確かに、反力の話って詳しく解説してなかったよね。新しく覚えることはあるの?

次回はいよいよ応力計算の話になるから、その準備みたいな感じだね。今回は、今まで学習した内容のおさらいがメインだから新しい話はないよ。
次回は断面力の話をする予定です。
支点反力の計算はそのための準備計算になります。力のつり合いについて振り返ってみましょう。
それでは早速始めます。
支点と反力

支点とは物体を支える場所のことです。
梁の場合、部材の両端に支える場所があるため、上に人やものが載ることができます。
支点に生じる外力のことを反力といいます。
よく勘違いしている人がいますが、反力は外力です。
反力がなぜ外力なのかというと、荷重がかかった時に地面や床(外部環境)から押し返される力だからです。
床の上に立っている時、両足に体重を感じますよね。あれが、支点反力です。
支点のパターン
支点はいくつか固定度の種類があります。
構造力学では主に3つの支点パターンを考えます。
- ローラー支点(移動支承)
- ピン支点(回転支承)
- 完全固定(固定端)
構造実務では、ピン支点と固定の間の固定度としてばねを設定することもあります。
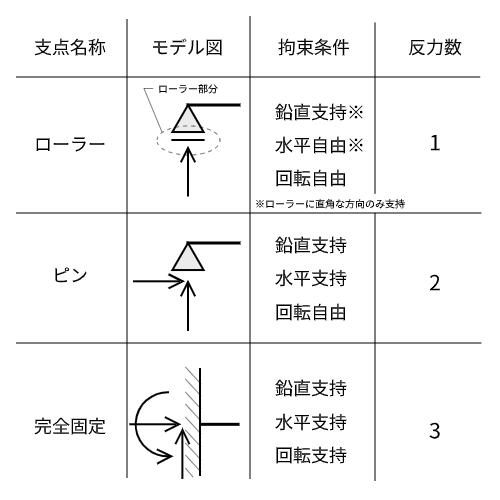
支点の拘束条件と反力
支点の拘束条件(境界条件)によって反力の数が変わります。
先ほどの3つの支点の場合、
- ローラー支点:ローラー方向は拘束されない。自由に回転できる
- ピン支点:回転のみ自由に動ける
- 完全固定:水平、鉛直、回転方向すべて拘束されている
という違いがあり、拘束の数だけ支点反力の数が増えます。
まとめると、以下の表のようになります。
反力の求め方
それでは、実際に反力を求める手順をご説明します。
この記事では、単純梁(集中荷重パターン)と片持ち梁(等分布荷重パターン)の2つの例で反力を求めてみます。
求める手順は次のとおりです。
- STEP 1支点反力を書く
- 試験問題の図に支点反力を書き込みます。
- 符号と力の正負は各自設定してください。
- STEP 2分布荷重を集中荷重に直す
- 問題に分布荷重があれば、集中荷重に変換しておきましょう。
- STEP 3つり合い式を立てる
- 3つの力のつり合い式を立てます。
- STEP 4反力を求める
- つり合い式の連立方程式を解いて反力を求めます。
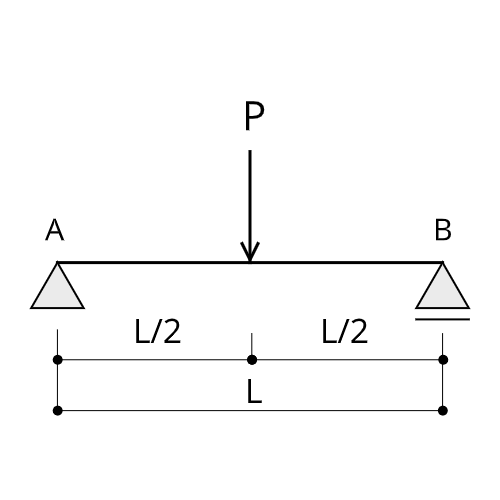
単純梁の場合
支点反力を書く
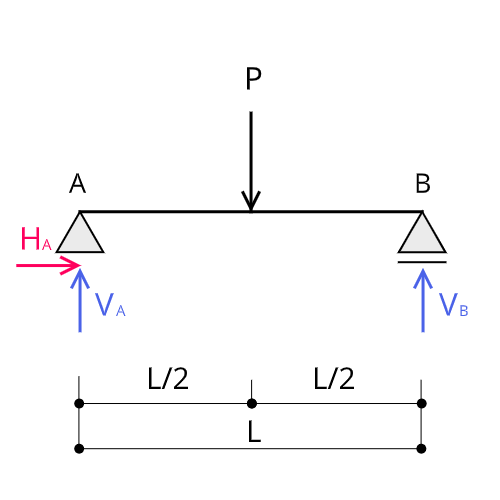
まず、支点反力を図に書き込みます。
A点はピン支点、B点はローラー支点となっているので、A点に水平反力$H_A$と鉛直反力$V_A$を、B点に鉛直反力$V_B$を書き込みます。
反力の向き(矢印の向き)は右向き、上向きを正(プラス)としました。
この向きについてはどちら向きに設定しても構いません。
この例題では分布荷重はないので、そのまま反力を求めます。
つり合い式を立てる
まず、力のつり合いを考えます。
つり合い式は、
- 水平方向のつり合い($\Sigma H = 0$)
- 鉛直方向のつり合い($\Sigma V = 0$)
- 回転方向のつり合い($\Sigma M = 0$)
の3種類の式を立てます。
この記号$\Sigma$(シグマ)は合計という意味で使っています。
・$\Sigma H = 0$
図を見ると水平反力以外に水平方向の外力がないため、$H = 0$です。
・$\Sigma V = 0$
上向きを正として、
$$V_A + V_B - P = 0$$
・$\Sigma M = 0$
時計回りを正として、支点Aを回転中心とした力のモーメントのつり合い式を立てます。
力のモーメントは(作用する力)×(支点からの距離)で求められます。
$$P \times \frac{L}{2} - V_B \times L = 0$$
反力を求める
3つのつり合い式の連立方程式を解くと、反力$V_A$と$V_B$が出てきます。
$$V_A = V_B = \frac{P}{2}$$
この例題の場合、計算しなくても直感的に荷重の半分の力$\frac{P}{2}$がかかると答えられると思いますが、計算の手順はしっかり確認しておきましょう。
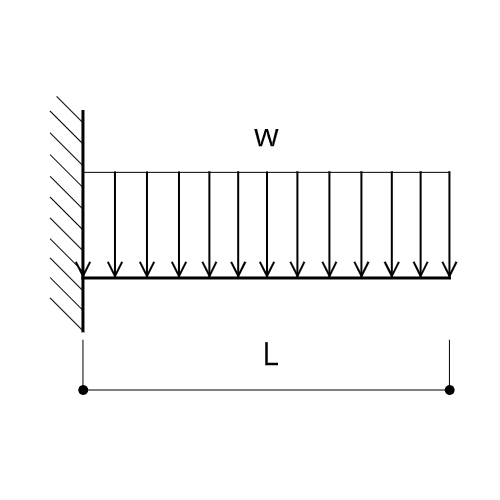
片持ち梁の場合
続いて、片持ち梁の場合についても反力を求めてみましょう。
支点反力を書く
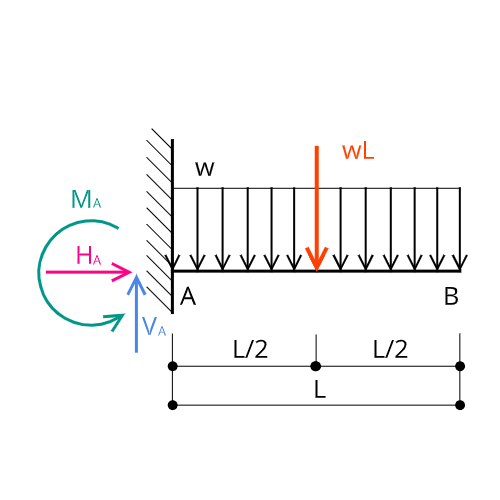
支点反力は図のようになります。
A点は固定端、B点は拘束がないので、A点に水平反力$H_A$と鉛直反力$V_A$、モーメント$M_A$を書き込みます。
反力の向き(矢印の向き)は右向き、上向き、反時計回りを正(プラス)にしています。
分布荷重を集中荷重に直す
この問題では荷重が等分布荷重なので、計算するときに集中荷重に直す必要があります。
力のつり合い式を立てるタイミング以降でこの作業をするのは計算ミスの元。
つり合い式を立てる前にやっておきましょう。
集中荷重に直すと、力の大きさ$wL$と位置(スパンの中央)を図に書き込んでください。
つり合い式を立てる
つり合い式は次のとおりです。
・$\Sigma H = 0$
こちらも、水平反力以外に水平方向の外力がないため、$H = 0$です。
・$\Sigma V = 0$
上向きを正として、
$$V_A - wL = 0$$
・$\Sigma M = 0$
時計回りを正として、A点を回転中心とした力のモーメントのつり合いから、
$$wL \times \frac{L}{2} - M_A = 0$$
反力を求める
3つのつり合い式の連立方程式を解くと、反力$V_A$と$M_A$が出てきます。
$$V_A = wL$$
$$M_A = \frac{wL^2}{2}$$
まとめ
お疲れ様でした。
今回は支点と反力の種類について例題を交えながら解説しました。
反力の計算は始めのうちは慣れないかもしれません。
しかし、たくさん問題をこなして上達していくのが勉強の正攻法です。
もし、途中のつり合い式や分布荷重でつまずいたという人は、以下の記事を参考にしてみてください。
参考記事その1 » 【構造力学の基礎】力のモーメント【第2回】
参考記事その2 » 【構造力学の基礎】分布荷重【第6回】
それでは、また。



































コメント