こんにちは、ゆるカピ(@yurucapi_san)です。
今回は「たわみとたわみ角」について解説していきます。
これまで力についてたくさん解説してきましたが、今回は変形の話になります。
先に言っておきますが、たわみ、たわみ角に関しては公式を暗記してしまったほうが早いです。
たわみ、たわみ角を真面目に求めようとすると、微分方程式を解く必要があるからですね。

つまり計算がめんどくさいから暗記したほうがいいって話です。
- 構造設計実務歴7年目(組織設計事務所)
- 大学院時代に構造力学のTAを経験、ほか構造力学の指導経験あり
- 一級建築士試験ストレート合格

もっと詳しく知りたい人はこちらにもまとめています。
- 曲げモーメントとたわみの関係
- たわみとたわみ角の関係
- よく出るたわみ、たわみ角の公式の覚え方
今回は試験によく出題される公式についても解説するので、少しばかりお付き合いください。

公式暗記の参考にどうぞ。
たわみってどんな現象?

たわみとは、荷重が作用した時に梁や床などが弓なりに変形することです。
あなたはこんな経験をしたことはないでしょうか?
- 古い民家の床を歩いてたらギシギシと音をたてながら床がたわんだ
- レジャーなどで使われるプラスチックの椅子の上に乗ったら座面が下がった
梁や床、椅子の座面など高さや厚みに対して水平面に広がりがあるものは、たわみが生じます。
たわみ制限
椅子に乗る時ぐにゃっと下がったり普段生活している床がトランポリンのように柔らかかったら、あなたはどう感じますか?

え、壊れるんじゃ・・・。常に揺れてたら気持ち悪くなっちゃうよね。

壊れないとわかっていても、やっぱり不安だよね•••。
建築基準法や学会の計算規準などでは、このような不快感を考慮してたわみを小さくするための制限が設けられています。
例えば、
- 梁のスパン$L$に対して、1/300や1/250以下
- 絶対量$20mm$以下(鉄骨梁の場合)
といったたわみの制限を設けます。
最近では、長期的なたわみだけでなく日常生活の歩行振動によるたわみを抑える設計もするケースが増えてきました。
曲げモーメントとたわみの関係
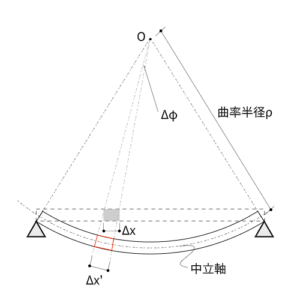
梁の中央に荷重がかかると、中央の位置が下がって弓なりに曲がります。
第5回の曲げモーメントでは、弓なりに曲がった変形を曲げモーメント$M$と曲率の式で表現していました。
$$\frac{1}{\rho} = \frac{M}{EI}$$
この式がたわみを求めるための式のベースになっています。
たわみ曲線の微分方程式
結論から言えば、曲げモーメント$M$と曲率半径$\rho$の関係式を1回分、積分をするとたわみ角が、2回積分するとたわみが出てきます。
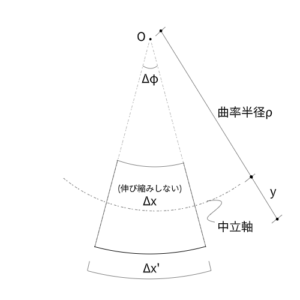
微分方程式で表すと、
$$\frac{d^2 y}{d y^2} = - \frac{M(x)}{EI}$$
となります。$x$と$y$の関係は上の図のとおりです。
ここで、あれ、と疑問に思いましたか?
そうです。微分方程式では右辺の頭に負(マイナス)の符号を入れています。
なぜ、負の符号をつけるのかというと、曲げモーメントの回転の向きと、たわみ、たわみ角の向きが反対になってしまうからです。
図を見てみましょう。
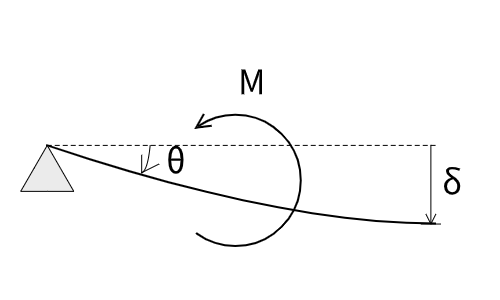
一般的に曲げモーメント$M$は引張を正(プラス)にとります。図の場合、反時計回りです。
一方、たわみは上から下に向けて増加し、たわみ角は図の場合、時計回りに回転変形します。
それぞれ回転方向が逆になるため負の関係になるわけです。
たわみとたわみ角の関係
たわみとたわみ角は微分積分の関係にあるとわかったところで、実現象の話に戻ります。
まとめると、
- 元の状態からどれだけ下がったのかを表したのが「たわみ」
- 部材の端からどれくらいの角度で下がったのかを表したのが「たわみ角」
ということです。
端部の固定条件(境界条件)で変わる
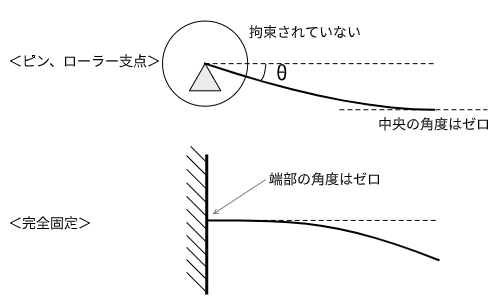
梁部材のたわみやたわみ角を考える時に気をつけないといけないのが、端部の固定条件です。
この固定条件のことを境界条件ともいいます。
固定条件がピンやローラー支点(蝶番のイメージ)の時は自由に回転できるため、荷重がかかると端部に角度が生じます。
固定条件が完全固定(壁に強力な接着剤をつけるイメージ)の時は、回転が拘束されているため、端部には角度が生じません。つまり、端部のたわみ角はゼロです。
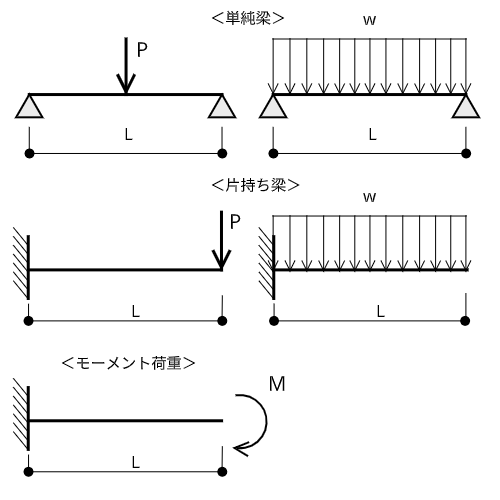
よく出るたわみ、たわみ角の公式
たわみ、たわみ角は、曲げモーメントを求めてから微分方程式を解けば求められますが、試験でもそのようなやり方をしていたら時間内に計算問題をこなすのは困難です。
なので、代表的な単純梁や肩持ち梁のたわみ、たわみ角は公式として覚えてしまったほうがいいでしょう。
じゃあ全部暗記だ、と意気込んでも全部覚えるのは大変です。

ある暗記苦手なんだよね〜。
そこで、効率的に覚える方法をお伝えしたいと思います。
たわみ、たわみ角の公式集
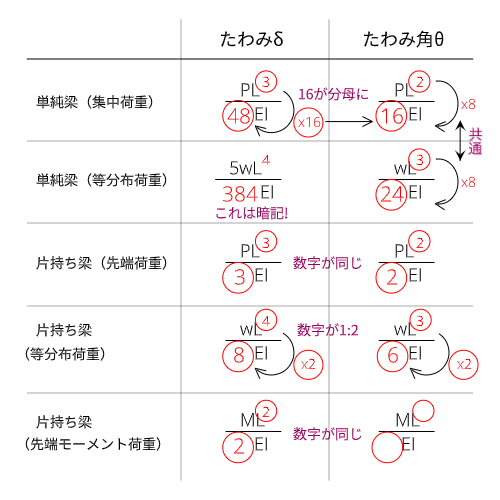
試験によく出題される公式集はこちらです。
| 梁の種類 | たわみ$\delta$ | たわみ角$\theta$ |
|---|---|---|
| 単純梁(集中荷重) | $\frac{PL^3}{48EI}$ | $\frac{PL^2}{16EI}$ |
| 単純梁(等分布荷重) | $\frac{5wL^4}{384EI}$ | $\frac{wL^3}{24EI}$ |
| 片持ち梁(先端荷重) | $\frac{PL^3}{3EI}$ | $\frac{PL^2}{2EI}$ |
| 片持ち梁(等分布荷重) | $\frac{wL^4}{8EI}$ | $\frac{wL^3}{6EI}$ |
| 片持ち梁(先端モーメント荷重) | $\frac{ML^2}{2EI}$ | $\frac{ML}{EI}$ |
記号やら数字やらいっぱい並んでいて見るのも疲れますよね。

こりゃあ、全部覚えるの大変だなあ・・・。
たわみ、たわみ角の公式の傾向
まず、たわみの公式にはいずれも以下の傾向があります。
集中荷重(片持ち梁は先端荷重)の場合
$$\delta = \frac{PL^3}{○○EI}$$
等分布荷重の場合
$$\delta = \frac{wL^4}{〇〇EI}$$
〇〇のところは単純梁なのか片持ち梁なのかによって数字が変わります。
集中荷重の時はスパン$L$の3乗、等分布荷重の時は4乗と覚えておくと楽です。
あとは分母に$EI$、分子に$P$や$w$などの荷重とスパン$L$が来ると覚えておけばOK。
またたわみとたわみ角は微分積分の関係にあるので、たわみ角の場合はスパン$L$の次数が1つずつ下がるだけで、そのほかの組み合わせは変わりません。
集中荷重(片持ち梁は先端荷重)の場合
$$\theta = \frac{PL^2}{○○EI}$$
等分布荷重の場合
$$\theta = \frac{wL^3}{〇〇EI}$$
この傾向をつかんだだけでも、少しは覚えるハードルが下がった気がしませんか?

パターン化すると覚えやすいかも。
おまけ
最後に、私自身が試験勉強の時になんとなく覚えたやり方を載せておきます。
覚える順番は、片持ち梁(先端荷重)のたわみ公式から始めるといいでしょう。
一番覚えやすいと思います。
次に単純梁のたわみ公式を覚えてしまいましょう。
たわみ角の公式はたわみ公式と紐づけて覚えるのが効率的です。
まとめ
お疲れ様でした。
たわみ、たわみ角は公式を覚えているかどうかで試験問題が解けるかが変わってきます。
暗記が得意な人にとってはボーナス問題ですね。
たわみ、たわみ角の公式の覚え方はぜひ参考にしてみてください。
それでは、また。




































コメント