こんにちは、ゆるカピ(@yurucapi_san)です。
こんな人のための記事です。

曲げモーメントって講義で教わったけど、数式ばっかりでなんか難しそう...。曲げ変形の流れをわかりやすく解説してほしいな。
「曲げモーメント」って構造力学のなかでめちゃくちゃ重要な話なんですが、数式とか記号とかよくわからない図ばっかりで気が滅入っちゃいますよね。
なので今回は、なるべく数式の細かな誘導はせずに本質的なところだけをまとめてみました。
- 構造設計実務歴7年目(組織設計事務所)
- 大学院時代に構造力学のTAを経験、ほか構造力学の指導経験あり
- 一級建築士試験ストレート合格

もっと詳しく知りたい人はこちらにもまとめています。
- 曲げ変形がどんな変形なのか
- 曲げモーメントと応力、ひずみはどうやって求めたらいいのか
- 断面二次モーメントとはなんなのか
実際、ほとんどの人にとっては試験で使える程度のことを覚えちゃえばOK。
あまり深く悩まずサクッと覚えちゃいましょう。
曲げ変形ってどんな変形
構造力学で考える変形は4つあります。
- 軸変形
- せん断変形
- 曲げ変形
- ねじり変形
今回はそのうちの曲げ変形を扱います。
軸変形、せん断変形については過去の記事を確認してみてください。
曲げ変形のイメージ
曲げ変形はどんな変形でしょうか。
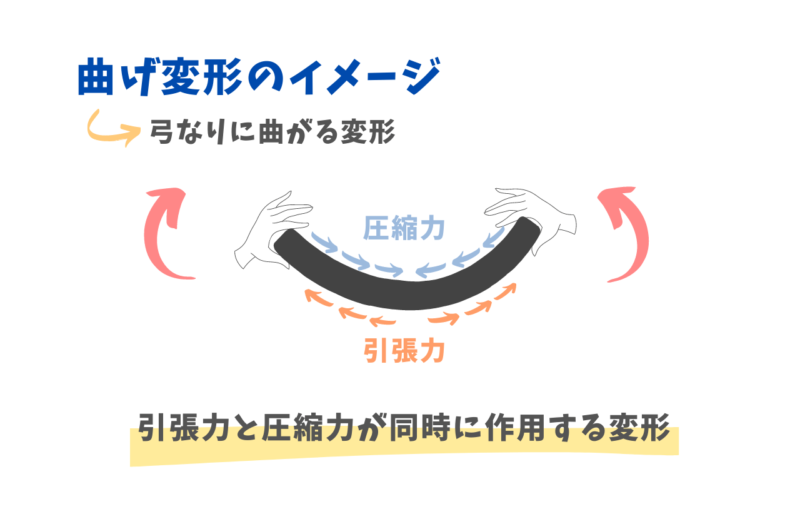
細長い棒の両端を持って曲げるように力を加えると棒は弓なりに曲がります。
このような弓なりに曲がる変形のことを曲げ変形と呼んでいます。
それでは、曲げ変形が生じた時に、その部材の内部にはどんな力のやりとりがあるのでしょうか。
例えば梱包材に入っている発泡スチロールの両端を持って曲げると、中央部のある側面から裂け始めるのを経験したことはあるでしょうか。
実は、裂け始めたほうには引張力が、その反対側には圧縮力が作用しています。
つまり、曲げ変形は、引張力と圧縮力が同時に作用する変形ともいえます。

ちょっと柔らかめな棒材があったら実際に曲げてみると理解しやすいよ。
力のモーメントと曲げモーメントの違い
本題に入る前に、第2回で取りあげた「力のモーメント」と「曲げモーメント」の違いについて簡単に説明します。
構造力学を学び始めの頃は、この2つのモーメントを混同しやすいです。
違いがよくわからずに試験で使っている人も多いと思います。

てっきり一緒だと思ってた•••。
どちらも同じ「モーメント」の名称がついていますが、簡単に言うと、力のモーメントは外力、曲げモーメントは部材の内部に作用する内力のことをいいます。
先ほどの発泡スチロールで例えるなら、手で発泡スチロールの両端にかけた力が力のモーメント、曲げた時に発泡スチロールに作用する内力が曲げモーメントです。
この違いを理解していないと、あとで解説する軸力・せん断力・曲げモーメントを合わせた断面力と外力との力のつり合いに対する理解が不十分になり、思わぬミスをしてしまいます。
2つのモーメントの違いについて、頭の片隅にでも置いておきましょう。
ひずみと曲率の関係
曲げ変形では引張力と圧縮力が同時に作用しているとお伝えしました。
例えば、梁部材中央の曲げ変形では、下側に引張ひずみ、上側に圧縮ひずみが生じています。
これは引張ひずみから圧縮ひずみに切り替わる、引張も圧縮も生じない部分もあることを意味しています。
$\varepsilon = 0$となる位置を中立軸と呼んでいます。
一方で、これは曲げ応力というひとつの応力に対して複数のひずみが生じていることを意味します。
たくさんの未知数がある
→ 応力とひずみの関係がよくわからない・・・
ということになってしまいます。
この問題を解決してくれるのが、平面保持の仮定という考え方です。

このあたりの用語はなんとなーくの理解で大丈夫です。
梁の変形に関する仮定
梁の変形に関して計算を簡単にするために以下のような約束事を決めています。
梁の変形に対して、
- 変形後も、部材に直角な断面は直角なままである。(平面保持の仮定)
- 変形後も、部材に直角な断面の形状は変化しない。(断面形状不変の仮定)
- 変形は微小である。(微小変位理論)
(出典:Wikipediaより抜粋、一部加工編集)
この仮定条件は詳しく説明すると数式だらけでわけがわからなくなるので、ここではざっくりとした説明とします。
1つ目は平面保持の仮定(あるいはベルヌーイ・オイラーの仮定)と呼ばれるもので、第4回でお話ししたようなせん断変形は考えません、というものです。
2つ目も結論的には1つ目と同じ話です。
3つ目は今回の話と直接関係はありませんが、今はたわみが大きくなりすぎると辻褄が合わなくなるよ、という理解で大丈夫です。
この仮定に基づくと、純粋に曲げ変形だけを考えればいいことになります。
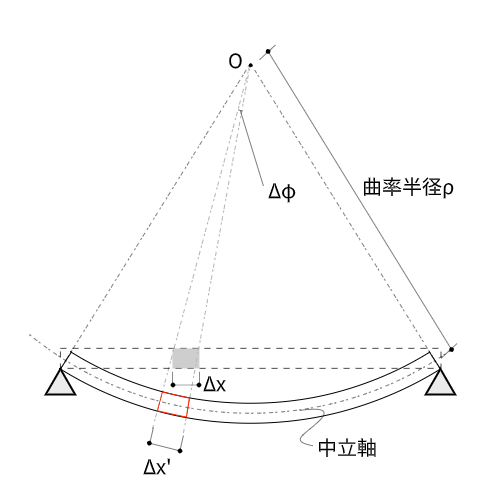
また、微小変形ということに着目して、この曲げ変形を円弧状の変形とみなすというのが、曲げに関するひずみを求めるうえで重要なカギとなります。
円弧状の変形とすると、梁の引張ひずみ、圧縮ひずみは断面内で一様の分布になります。
曲げに関するひずみは、ある点を円の中心とした円弧の回転角$\delta \phi$の変化率と考えることができます。
この変形は厳密には3次曲線なのですが、円弧で考えたほうがはるかに便利なので、微小変形の範囲に限定して使っています。このあたりは工学的な発想ですね。
ひずみを求めてみる
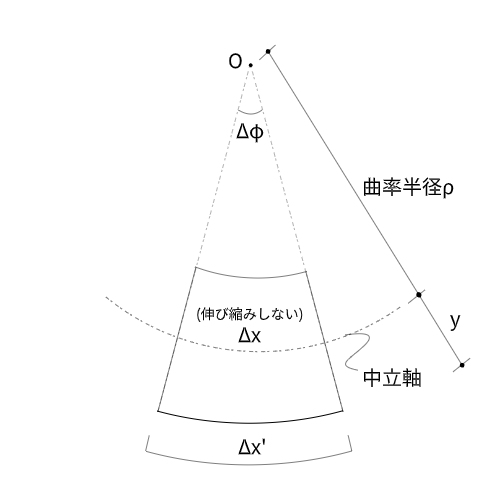
長方形から台形状の形に変化した時のひずみは、水平方向の変位から求めることができます。
$$\varepsilon = \frac{\Delta x' - \Delta x}{\Delta x} = \frac{\Delta x'}{\Delta x} - 1$$
また、曲率半径$\rho$(ロー)、中立軸からの任意の距離$y$を使って同じようにひずみを求めることができます。
$$\rho : \Delta x = ( \rho + y ) : \Delta x'$$
$$\rho \Delta x' = \Delta x ( \rho + y )$$
$$\frac{\Delta x'}{\Delta x} = \frac{\rho + y}{\rho} = 1+ \frac{y}{\rho}$$

数式と記号ばっかりで難しいと思うかもしれないけど、やってるのは相似の比較だけ。がんばって!
先ほどの$\varepsilon$の式に代入すると、
$$\varepsilon = 1 + \frac{y}{\rho} -1 = \frac{y}{\rho}$$
という式が出てきます。
これで、ひずみ→曲げ応力、曲げ応力→曲げモーメントの導出へのステップの準備ができました。

たぶん、これが一番単純にひずみと曲率の関係を導き出す方法じゃないかな。
曲げ応力を求める
ひずみが求められたので、早速フックの法則に従って曲げ応力を求めます。
$$\sigma_b = E \varepsilon = E \frac{y}{\rho}$$
$\sigma$の添字$b$は英語の「bend」からきています。
軸応力と見分けるためにつけます。
曲げモーメント$M$からのアプローチで、曲げ応力$\sigma_b$との関係を見てみましょう。
軸応力を求める時は引張力や圧縮力を断面積で割って求めていました。
同じように、曲げモーメントを求めるために曲げ応力に断面積を掛けるとしたいのですが、中立軸を境に引張から圧縮に切り替わるため少し工夫が必要です。
方法としては、曲げ応力と微小面積の積に中立軸からの距離$y$を掛ける、いわゆる積分を行います。

積分はちょっと苦手だなあ•••。

難しいから考え方だけ説明するよ。細かい計算過程が知りたい人は参考書を読んでね。
曲げモーメント式の考え方
結果の式は以下のようになります。
$$M = \int_{A}^{} \sigma_b y dA$$
まず、力のつり合いから考えていきましょう。
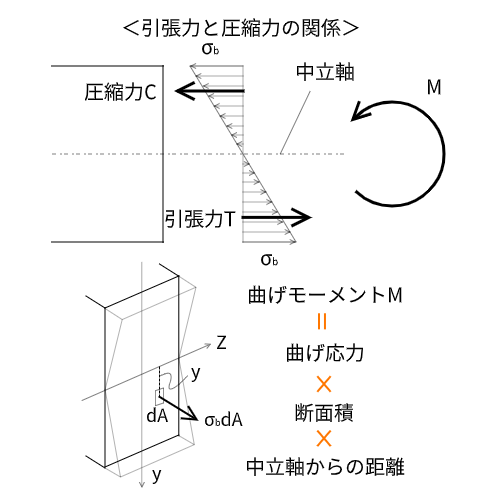
梁断面には引張力と圧縮力が合わさって曲げモーメントが生じています。
引張力の合計と圧縮力の合計はつり合っているので(じゃないと別の曲げモーメントか軸力がかかっていることになる)、偶力と考えることができます。
力に距離を掛けてモーメントのつり合いを考えると、偶力とそのモーメントとの関係がわかります。
同じように、任意の位置の(曲げ応力×断面積×中立軸からの距離)で曲げモーメントを求めることができるということです。
曲げ応力まとめ
求められた曲げモーメントの式にひずみの式を代入してみると、
$$M = \int_{A}^{} \frac{E}{\rho} y^2 dA = \frac{EI}{\rho}$$
または、
$$\frac{M}{EI} = \frac{1}{\rho}$$
となります。ただし、$I = \int_{A}^{} y^2 dA$とします。
まとめると、
$$\sigma_b = \frac{Ey}{\rho} = \frac{M}{I} y$$
です。おなじみの曲げ応力$\sigma_b$の式が出てきました。

この導出過程は何回か練習しておくと試験で応用が効くよ。
断面2次モーメント
先ほどの計算途中に$I$を設定しました。これを断面二次モーメントといいます。
よく、断面二次モーメントがよくわからないという質問を受けます。
結論を言うと、これについてはあまり深く考える必要はありません。
というのも、断面二次モーメントはただの計算過程で出てきた副産物にすぎないからです。
たまたま出てきたものを実務で使ってみたら、部材の曲げに対する固さ(曲げ剛性)をうまく評価できたということなのです。
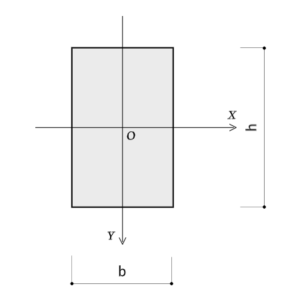
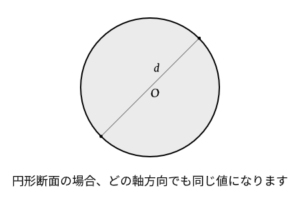
試験対策としては、よく出題される長方形断面と円形断面の断面二次モーメントの公式を覚えておけば大丈夫です。
具体的な計算はどうしたらいいの?という人は、計算例を解説している断面諸量に関する記事が参考にしてみてください。
まとめ
お疲れ様でした。
今回はいつもよりボリュームが多くて読むのに時間がかかったのではないでしょうか。
重要な内容ですが一度に理解するのは大変だと思います。
私自身ひずみと曲率のところは勉強していた時かなり苦戦したのを憶えています。
構造力学の勉強をしていて少しでも参考になったら幸いです。
それでは、また。
分布荷重の基本的な考え方、分布荷重→集中荷重への変換の仕方などを解説しています。





































コメント