こんにちは、ゆるカピ(@yurucapi_san)です。
今回は「せん断」について解説していきます。
「せん断」という単語は構造力学を勉強しない限りなかなか聞かない単語です。
それくらい馴染みのない話なので、しっかり意識して学習しておきましょう!
- 構造設計実務歴7年目(組織設計事務所)
- 大学院時代に構造力学のTAを経験、ほか構造力学の指導経験あり
- 一級建築士試験ストレート合格

もっと詳しく知りたい人はこちらにもまとめています。
- せん断変形とはどんな変形なのか
- せん断力と変形にはどんな関係があるのか
私は大学院生時代、何人もの建築学生の後輩からの構造力学に関する質問に答えてきました。
- 多くの人が詰まりそうなところ
- 割り切って覚えるべきところ
などを初心者向けのアドバイスができます。

構造力学勉強し始めたけど、さっぱりわからない...。
こんな人の参考になれば幸いです。
それでは、早速始めていきます。
せん断変形ってどんな変形?
せん断変形とはどんな変形でしょうか。
まずは前回のおさらいから。
前回の内容があやふやだなという人は「【構造力学の基礎】引張、圧縮【第3回】」という記事を復習しておいてください。
構造力学では、4つの変形があり、そのうちのひとつにせん断変形があります。
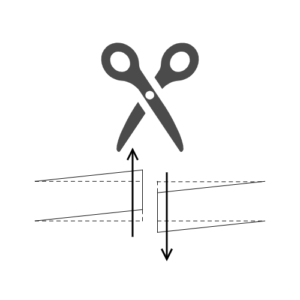
せん断変形とは、例えばハサミでねじ切るような変形のことをいいます。
ハサミの上刃と下刃にはそれぞれ上下の力がかかり、切り取る紙の部分は上下に分断されますよね。
この時の上下にずれる変形がせん断変形です。
別の例でいうと、紙の資料に穴を開ける2穴パンチの場合も同じ。
上からパンチの刃で押し込むと円形の穴が開きますよね。
これもせん断変形を利用したものです。
何枚も積み重なった紙に一度に穴を開けると、一番上の紙の表面にはめり込んだような状態、一番したの紙の裏側には開けた円周部分がめくれ上がったような状態になりますよね。
このような変形がせん断変形です。
せん断ひずみ
こちらもまずは前回の「引張、圧縮」のおさらいから入りましょう。
引張や圧縮の時、ひずみ$\varepsilon$は元の長さに対する割合で表現できました。
せん断変形はこの変形とは違うため、新しくせん断ひずみとして考えます。
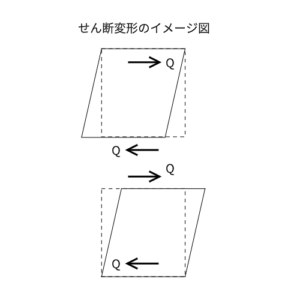
図のような変形ですね。
この時どのように変形の度合いを評価すればいいかというと、
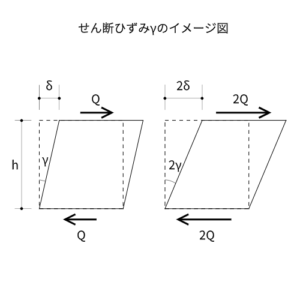
図のように平行四辺形の傾きで考えます。
つまり、水平変形$\delta$と傾き$\gamma$(ガンマ)は比例しています。
これを式に表すと、
$$\gamma = \frac{\delta}{h}$$
です。
フックの法則に合わせてみる
せん断変形についても、引張、圧縮の時に定義したフックの法則のような比例関係の式で表せます。
$$\tau = G \gamma$$
ここで、せん断応力を$\tau$(タウ)、せん断弾性係数を$G$とします。
$G$はヤング係数$E$と同じようなものだとして、$\tau$はどんな応力なのでしょうか。
せん断応力
せん断応力$\tau$は、軸応力$\sigma$が$\sigma = N / A$だったように、
$$\tau = \frac{Q}{A}$$
で表せます。
$Q$はせん断力と呼ばれ、切断面に作用する内力を表しています。
単位面積あたりというのは軸応力と共通しているので、
- 切断面に対して直角に作用する応力=軸応力
- 切断面に平行に作用する応力=せん断応力
と考えることもできます。
詳しくは主応力の話になるのでここでは触れないこととします。
↓Wikipediaの記事ページを参考リンクに貼っておきます。興味がある人はこちらからどうぞ↓
せん断弾性係数とヤング係数の関係
せん断弾性係数$G$とヤング係数$E$はいずれも材料特性を表す係数です。
この2つの係数の関係について簡単に解説します。
2つの式はポアソン比という考え方を利用して求めることができます。
ポアソン比は、物体を上から押し込んだ時につぶれて横に広がる現象を数式で表したものです。
粘土や発酵してこねたパンを上から押さえつけたらペシャンコに広がりますよね。
計算過程は少し難しいので触れませんが、計算していくと下式のようになります。
$$G = \frac{E}{2(1+\gamma)}$$

わりと有名な式だから覚えてしまってもいいかも。
材料ごとのヤング係数とせん断弾性係数
コンクリートの場合、ポアソン比$\gamma = 0.2$、ヤング係数$E = 21,000 N/mm^2$とすると、
$$G = \frac{21,000}{2 \times (1 + 0.2)} = 8,750 N/mm^2$$
です。
鋼材の場合、ヤング係数$E = 205,000 N/mm^2$、$G = 79,000 N/mm^2$とすることが多いです。
梁のせん断応力
せん断応力は$\tau = Q / A$で表せます。
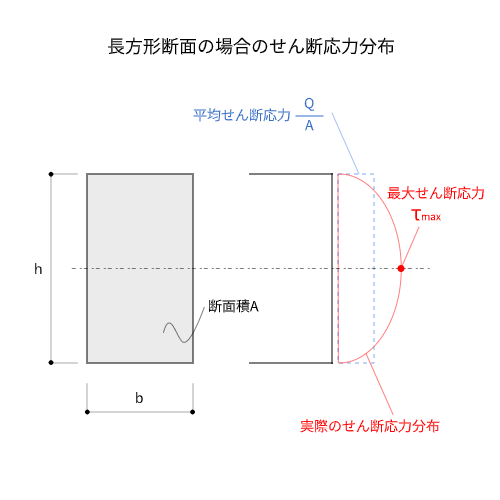
しかし梁のような長方形断面で考えた時、実際のせん断応力は図のような円弧状の応力分布になります。
これでは単純にせん断力を断面積で割った値とはなりません。
あくまで$Q / A$は円弧状の分布を長方形分布に均した平均応力分布ということです。
実情に合わせて断面の両端の応力は小さく中央は大きくなるように修正すると、
$$\tau = \frac{Q S}{b I}$$
となります。
$Q$はせん断力、$S$は断面一次モーメント、$b$は断面の幅、$I$は断面二次モーメントです。
断面二次モーメントについては「【構造力学の基礎】断面諸量【第10回】」の記事で解説しています。
梁断面中央の最大せん断応力
梁断面の中央の最大せん断応力は、$Q / A$と比べてどれくらいになるでしょうか。
幅$b$、高さ$h$、断面積$A$の断面形状とし、断面の中央位置の断面一次モーメントを$S = bh^2/8$、断面二次モーメントを$I = bh^3/12$とすると、
$$\tau = \frac{Q \times (\frac{bh^2}{8})}{b \times (\frac{bh^3}{12})} = \frac{3}{2} \times (\frac{Q}{bh}) = 1.5 \times \frac{Q}{A}$$
となります。
長方形断面の場合平均せん断応力は$Q / A$なので、最大せん断応力は平均の1.5倍であることがわかりました。
誤解のないように言っておくと、ほかの断面形状の場合は断面一次モーメント$S$と断面二次モーメント$I$が変わるので、必ずしも平均の1.5倍とは限りません。
長方形断面の最大せん断応力を求める時は必ず1.5倍するのを忘れないようにしましょう。

これは意外と忘れる人が多いです。
建築士試験では解答の4択のうち2択が1.5倍していない選択肢になっていることも少なくありません。
絶対に忘れないようにしましょう。
まとめ
お疲れ様でした。
せん断変形は構造力学を勉強して初めて知ったという人も多いと思います。
まさに私自身がそうでした。
数式がたくさん出てきて難しく感じてしまいますが、試験で出てくる部分はそれほど難しくありません。
応力、ひずみの関係式などは暗記してしまったほうが早いでしょう。
実際の現象と合わせて覚えると理解は深まるはずです。
一度で理解するのは大変なので都度繰り返し復習しながら覚えていきましょう。
それでは、また。




































コメント