こんにちは、ゆるカピ(@yurucapi_san)です。
今回は第18回のオイラー座屈の話を少し深掘りしたいと思います。
>>オイラー座屈の記事はこちらから読めます。
おそらく、これを読んだだけだと、単純な柱の座屈の問題は解けるけどラーメン構造になっている問題は解けないかもしれません。

内容の補足も兼ねて深掘りしたいと思います。
もちろん、オイラー座屈の知識は建築士試験に合格するためには必須なので、理解があいまいな人はぜひ復習しておいてください。
私の簡単なプロフィールです。
- 構造設計実務歴7年目(組織設計事務所)
- 大学院時代に構造力学のTAを経験、ほか構造力学の指導経験あり
- 一級建築士試験ストレート合格

もっと詳しく知りたい人はこちらにもまとめています。
もともと構造力学は苦手なほうでしたが、勉強を重ねて今では人に教えられる程度には習得しているレベルに到達しています。
今回のテーマである骨組の座屈は、基本的には柱の座屈が理解できていれば問題ありません。知らないとつまずくかも、というレベルの応用です。
- 簡単な座屈モードがわかる
- 建築士試験問題で気をつけるポイントがわかる
- 剛でない梁の場合の座屈の問題を解くポイントがわかる
それでは、早速始めていきます。
柱の座屈モードをおさらい
細長い長柱のような部材は圧縮力を受けると弓なりに変形します。柱の固定条件によって曲がり方が変わります。これが柱の座屈モードです。
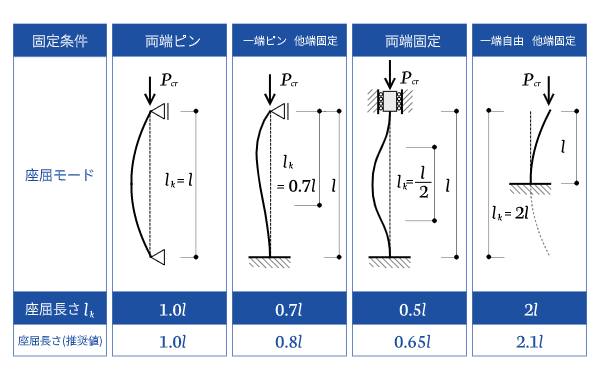
柱の端部の固定条件が、ピンや自由端のように拘束されなくなると座屈長さが長くなり、少ない座屈荷重で座屈する傾向があります。
骨組の座屈モードはこんな感じ
ラーメン骨組の座屈モードでは、
- 水平移動が拘束されている場合
- 水平移動が拘束されていない場合
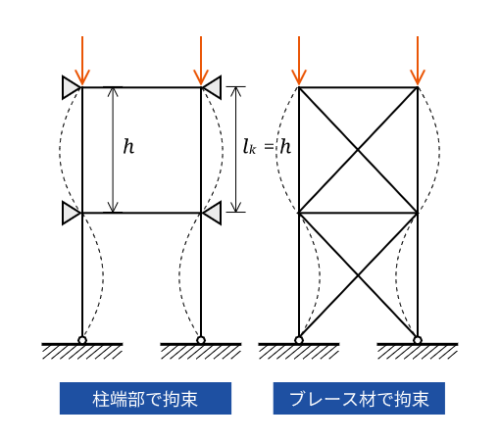
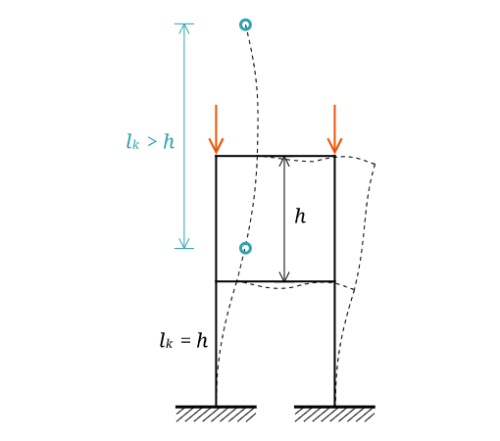
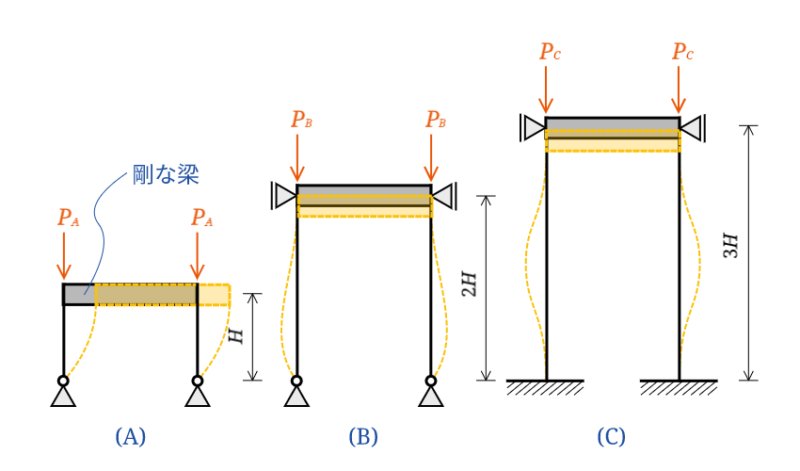
の2種類に分けて考えます。下図のようなイメージです。
水平拘束がないと、座屈長さがかなり長くなってしまうことがわかります。節点間距離の3倍に達するという話もあります。
梁や床スラブの剛性もあるので、実際の座屈変形挙動は拘束ありと拘束なしの間になります。
また、図では均等に座屈する前提で座屈モードを描いていますが、実際は不均等なのでこんなきれいな変形にはなりません。
あくまで、単純化したらこうなる、と考えてください。

構造系の研究では固有値解析で最適な評価方法を提案していたり、いろいろ奥が深くて難しくなっちゃうので詳細は省くよ。
骨組の座屈で出題されるタイプ 3種
過去に建築士試験で出題されたのは大きく分けて3種類あります。
- 柱の断面形状や固定条件の違いから座屈荷重の大小を答えるタイプ
- 座屈荷重に関する説明文で適当・不適当な答えを選ぶタイプ
- 剛ではない梁の場合の骨組の座屈荷重の大小を答えるタイプ
1つ目と2つ目についてはオイラー座屈の公式と固定条件による座屈長さの違いを知っていれば、問題なく解けると思います。
少し厄介なのは3つ目です。
後述しますが、剛ではない梁の場合は簡単に座屈荷重が求められないので、あらかじめ、おおよその大小関係を知っておいたほうがいいでしょう。

みんなが知りたいのはこの辺の話だよね。順を追って説明していくよ。
柱の断面形状や固定条件から座屈荷重を求める問題
このタイプの問題は、
- 問題文にある図に座屈モードを描き込む
- 変化しているパラメータだけ抜き出して計算する
- 座屈荷重を比較する
の順番でやるのがおすすめです。
先にオイラー座屈の公式を当てはめてしまうと、座屈モードが違っていた場合に手戻りになってしまうからです。
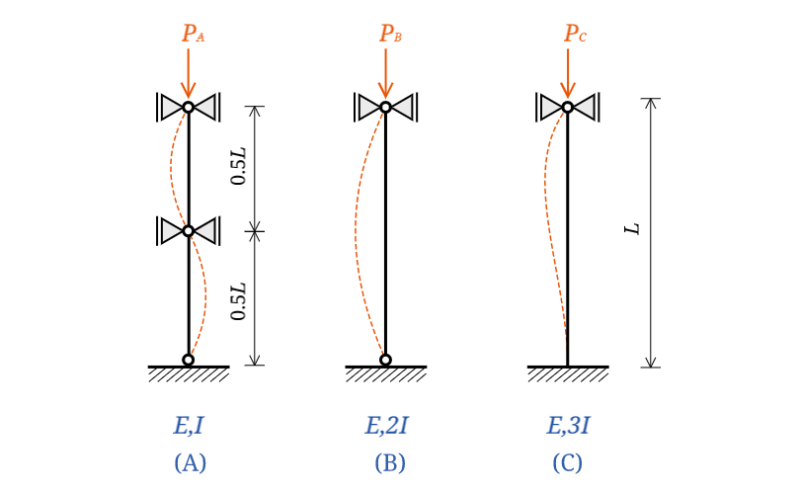
例えば、下図を見てみましょう。
これは平成14年の過去問をベースに作成したものです。
$(A)$の真ん中に水平移動拘束の支点があることを忘れて公式に当てはめると、誤った座屈モードで計算してしまうことになります。
計算は変化しているパラメータだけで行う
この問題の場合、変化しているパラメータは座屈長さ$l_k$と断面二次モーメント$I$だけです。なので、この2つだけを取り出して計算します。
$$A : \frac{I}{(0.5L)^2} , B : \frac{2I}{L^2} , C : \frac{3I}{(0.7L)^2}$$
数字だけ抽出すると、$P_A = 4 , P_B = 2 , P_C = 6.12$となるので、
$$P_C > P_A > P_B$$
の順に座屈荷重の大小関係が求められます。
試験では座屈荷重の大小関係を求める場合がほとんどなので、オイラー座屈の公式をなんとなく覚えているだけで解けてしまいます。

分母分子の関係、座屈長さを2乗することを覚えておけば解けるから、ある意味サービス問題だね!
座屈荷重に関する説明文の正誤問題
このタイプの問題を解く時は、まず最初にオイラー座屈の公式を問題文の脇にでも書き込みましょう。
$$P_{cr} = \frac{\pi^2 EI}{l_k^2}$$
公式に出てくるパラメータはヤング係数$E$、弱軸方向の断面二次モーメント$I$、座屈長さ$l_k$だけなので、この3種類の比例関係を問う問題が出題されます。
あとは座屈長さに関連して、柱の固定条件による違いを問う問題もあります。その時は、焦らずに柱の座屈モードの図を描いて座屈長さを比べてみるといいでしょう。

文章題だとイメージがつかみにくいし間違えるもとだから、積極的に図を描くようにしよう。
剛ではない梁の場合の骨組の座屈荷重の大小を求める問題
剛な梁の場合は、図のような座屈モードになるのでほかの座屈の問題と同じように解けます。
しかし、剛な梁ではない、となると事情が変わります。
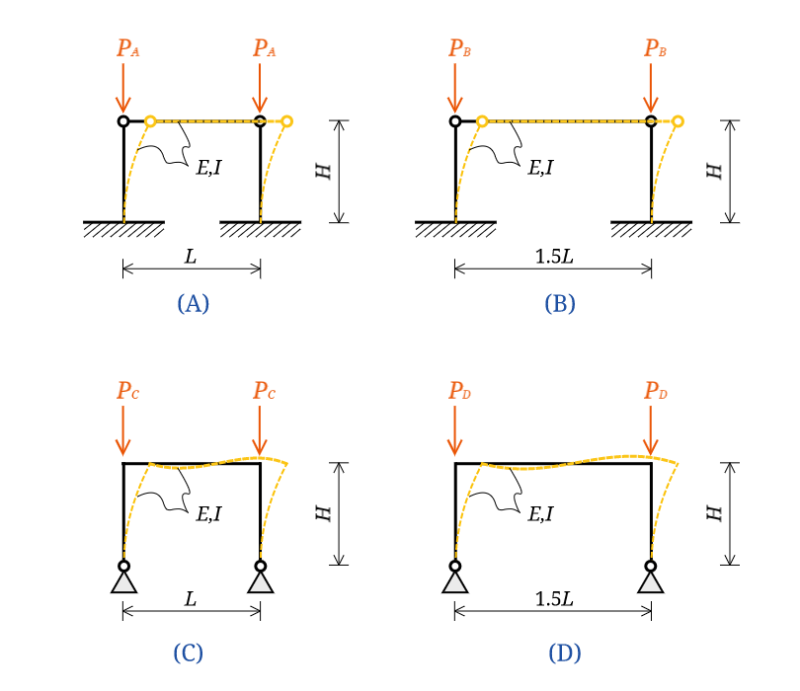
例えば、平成19年の過去問で考えてみましょう。
構造物$A,B$については、柱脚が剛接合、柱梁接合部がピン接合になっているので、一端自由・他端固定の座屈長さだとわかります。
よって、$P_A = P_B$です。

え?スパンの違いはないの?

構造物$A,B$はどちらも柱梁接合部がピン接合になってるから、梁の剛性の影響を受けないんだよ。
厄介なのは構造物$C,D$のほうです。
この時考えるポイントは、以下のとおりです。
- 固定条件がゆるくなると座屈長さは長くなる→座屈荷重:小
- 剛度$I/L$の割合で考える
固定条件を比較する
例えば、構造物$A$と$C$を見比べてください。
$A$の柱はピン-固定端の組合せなのに対して、$C$はピン-ラーメン接合の組合せです。ラーメン接合は固定端より固定度が低いため座屈長さは長くなります。
座屈長さが長くなる、ということは座屈荷重は小さくなりますね。
よって、$P_A = P_B > P_C$となります。
剛度$I/L$を比較する
剛度と聞くとなんだか難しそう、と戸惑うかもしれません。新しく覚えたくない人は曲げ剛性$EI/L$で考えてもOKです。
部材の断面二次モーメントが大きく、長さが短いと剛度が大きくなります。
この問題だと断面二次モーメントはすべて同じ大きさなので、スパンの違う$C$と$D$で考えてみましょう。
$D$は$C$の1.5倍のスパンなので、梁の剛度は1/1.5 = 2/3倍になります。梁の剛度が下がった分だけ柱頭の固定度も低くなるので、座屈荷重は$C$より小さくなります。
よって、$P_A = P_B > P_C > P_D$という大小関係が求められました。
梁の影響による座屈荷重の違い
梁の影響による座屈荷重の大小関係は以下のようになります。
剛な梁>ラーメン接合(スパン小)>ラーメン接合(スパン大)>ピン接合

ラーメン接合は剛とピンの間のイメージを持ってもらえればOKだよ。
まとめ
お疲れ様でした。
今回の内容、ちょっとマニアックな感じですが、建築士試験の構造の問題はバッチリおさえておきたいという人はしっかり復習しておいてください。
そもそも、断面力の計算とかトラスの計算でつまずいているという人は、そちらのほうを優先してください。以下に関連記事を載せておきます。
それでは、また。


































コメント