こんにちは、ゆるカピ(@yurucapi_san)です。
あなたは、塑性崩壊の問題ってなんとなく難しそう、と思っていませんか。
梁とかラーメン構造の崩壊荷重の問題って、言葉の響きが難しそうだし、参考書も難解な用語がたくさん出てくるのでとっつきにくいですよね。
でも、二級建築士ならいざ知らず、一級建築士試験の構造力学では必須な知識なんです。建築基準法でも保有水平耐力計算の話が出てきて、保有水平耐力計算は塑性の考え方が前提になっているもんだから、こりゃ、避けて通れないなとなるわけです。

別に構造力学得意じゃないのに、困ったな...。どうしよう。

試験問題を解くだけなら、ポイントさえおさえてれば大丈夫だよ。
今回は、そんなお悩みにお応えすべく、崩壊荷重の問題の解き方を解説したいと思います。
今回の話の前提として、そもそもの塑性変形の知識が必要です。塑性ってなに?という人は別で解説しているのでこちらの記事もどうぞ。
それでは始めます。
塑性ヒンジ状態ってどんな状態?
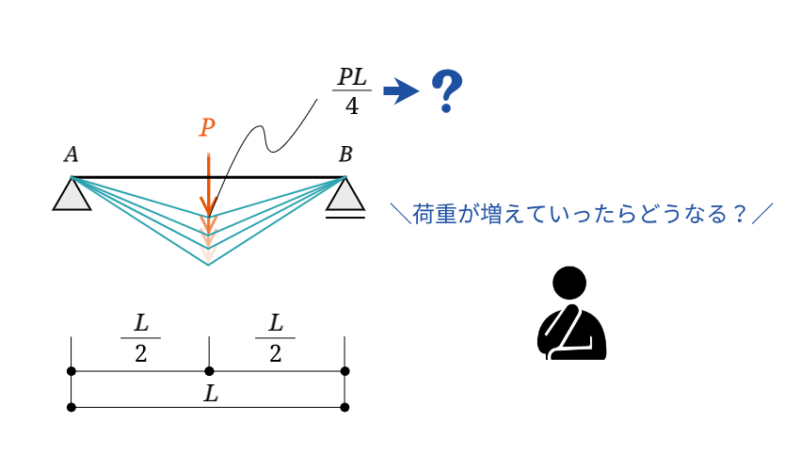
単純梁の集中荷重$P$を大きくしていくと、やがて部材の最大曲げモーメントが全塑性モーメント$M_p$に達します。梁中央の最大曲げモーメントが$M_P$に達した時の最大荷重$P_{max}$は次のように表せます。
$$M_p = \frac{P_{max} L}{4} \Leftrightarrow P_{max} = \frac{4 M_p}{L}$$
それでは、全塑性モーメントに達した後はどうなるか、というと全塑性モーメントはそのままで変形だけが進み、最終的に完全に崩壊します。
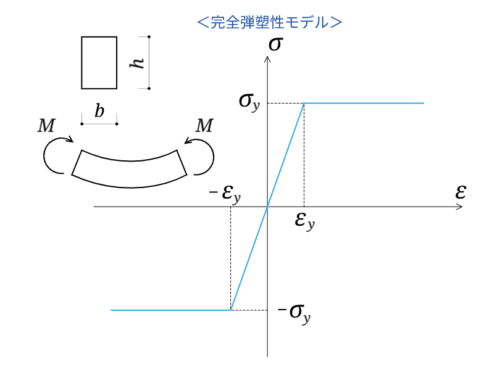
完全弾塑性の応力-ひずみ関係の図を見てみましょう。降伏応力$\sigma_y$に達した後はひずみ、すなわち変形だけが進んでいることがわかります。
このように、荷重が一定のまま変形だけが進むことを塑性崩壊と呼んでいて、塑性ヒンジが発生した状態のことを崩壊機構といいます。
一級建築士試験では崩壊機構から読み解いて、崩壊荷重$P_c$を求める問題が出てきます。

塑性崩壊とか崩壊機構とか、なんか難しそう...。

崩壊荷重を求める手順さえおさえていればいいよ。細かい話は深く掘り下げなくても大丈夫。
崩壊機構のイメージができたところで、続いて実際にどういう手順で解いたらいいかを解説します。
問題の解き方3ステップ

一級建築士試験に登場する崩壊荷重の問題は、次の3ステップを意識すれば求められます。
- 崩壊機構を考える
- 崩壊機構の図を描く
- 仮想仕事式を立てる
いきなり崩壊荷重を求めるとなると先が見えなくて途方にくれますが、流れを細分化するとわかりやすくなると思います。
崩壊機構を考える
崩壊荷重を求める問題は、不静定構造の場合がほとんどなので(たぶん先ほどの説明にあった単純梁くらい?)、真面目に解いて曲げモーメント図を描いて全塑性モーメントから崩壊荷重を求めていくのは大変です。

ここで書いてまとめただけで大変そう...。
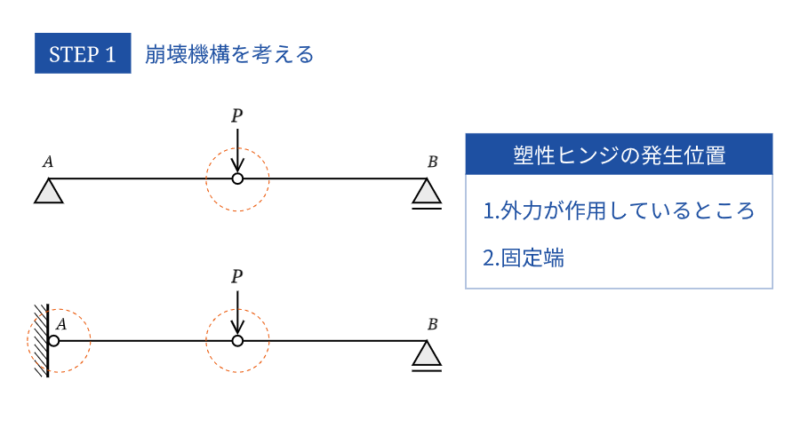
なので、曲げモーメントを求めないで崩壊機構のイメージを描いてみるのがいいでしょう。崩壊機構を描くためには塑性ヒンジの発生位置をおさえておく必要があります。塑性ヒンジは、
- 外力が作用しているところ
- 部材の固定端
の2箇所に発生します。まとめると、部材の中で曲げモーメントが大きくなる位置に塑性ヒンジが発生するということです。
全塑性モーメントは部材の断面で決まっていて、元々曲げモーメントが大きくなる位置は少ない力で塑性ヒンジが形成されるためです。
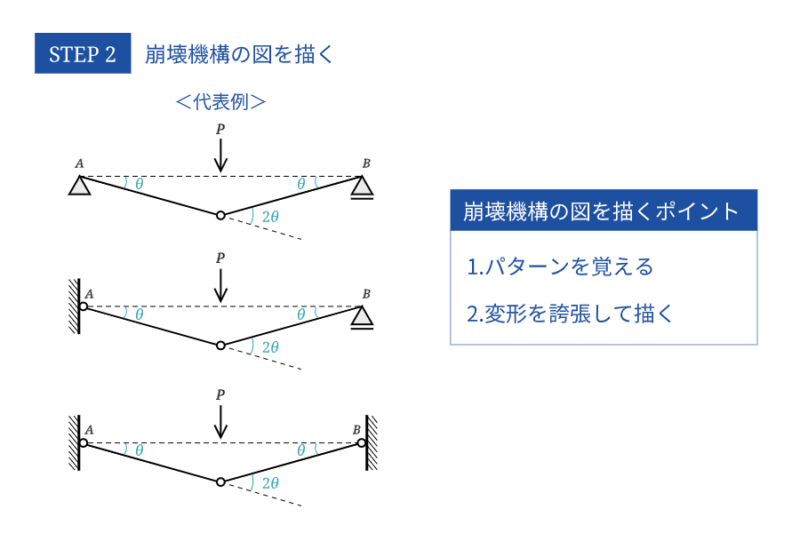
崩壊機構の図を描く
塑性ヒンジの位置を決めたら、早速崩壊機構の図を描いてみましょう。崩壊機構の図というのは、外力によって部材に塑性ヒンジが発生した時の変形図のことです。
曲げモーメントも求めてないのに変形図なんて描けないよと思うかもしれませんが、これはぶっちゃけ慣れの話なので、試しに描いてみてすぐに解答例を見て覚える、でいいと思います。
崩壊荷重の問題で出てくる崩壊機構の例もそれほど数は多くないので、崩壊機構の図のパターンを覚えちゃうのが一番早いです。
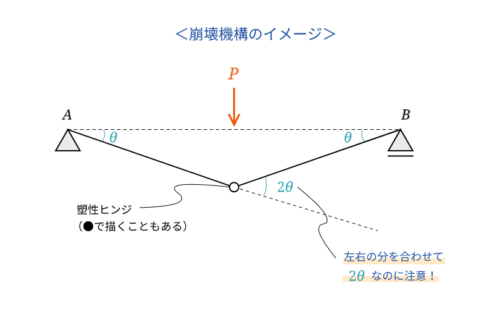
ひとつ描き方にポイントがあります。それは、手描きで描く時は解答例以上に変形を誇張して描く、ということです。誇張して描くと、$\theta$の開き具合も大きくなるので、$\theta$で書くべきところと$2 \theta$で書くべきところがわかりやすくなります。
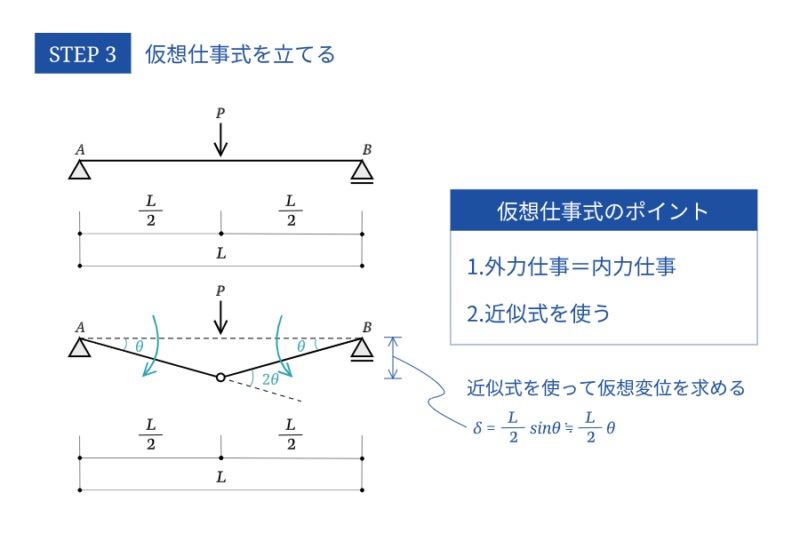
仮想仕事式を立てる
仮想?仕事?なんのこと?と思うかもしれません。
構造力学では、
部材が変形した = 変形した分エネルギーを消費した = 仕事した
と表現します。なので、
外力による仕事(外力×仮想変位)= 内力である曲げモーメントがなす仕事
という仮想仕事式と呼ばれる式が成り立ちます。

エネルギー一定の法則ともいえるね。
式で表現すると、
$$\Sigma P_c \times \delta_c = \Sigma M_p \times \theta$$
となります。単純梁(集中荷重)場合は$\delta_c$の部分を$(L/2) \theta$と表せるので、結果的に$\theta$が消えて崩壊荷重が求められるようになります。
梁の崩壊荷重を求めてみよう!
解き方の手順をもとに実際に問題に挑戦してみましょう。
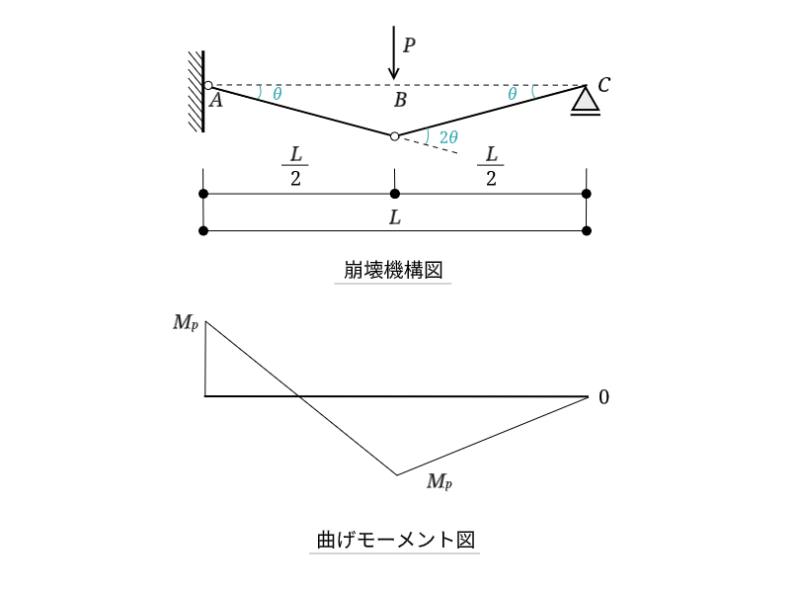
図の問題の反力を求める方法は別の記事で紹介しています。参考として、曲げモーメント図も載せておきます(今回は使いません)。
崩壊機構を考えて図に反映させる
この問題の塑性ヒンジの発生位置と、崩壊機構の図は次のようになります。説明で描いてるやつと同じです。
崩壊荷重を求める
点$A$および点$B$に塑性ヒンジが発生する時の崩壊荷重$P_c$を求めましょう。まずは崩壊機構図をもとに仮想仕事式を立てます。
式の左辺である外力仕事式は、
$$P_c \times \delta = P_c \times \frac{L}{2} \theta$$
となります。$\sin \theta \fallingdotseq \theta$という近似式を使うのがポイントです。
続いて、右辺の内力仕事式について考えてみます。ここで考えるのは、塑性ヒンジが発生しているところの全塑性モーメント$M_p$と、ヒンジの仮想回転量$\theta$の2つです。
中央部分は点$A$と点$C$の2方向から回転を受けるので、足されて$2 \theta$の回転量になります。式で表すと、
$$M_p \theta (Aの部分) + M_p 2 \theta (Bの部分) = M_p 3 \theta$$
となります。左辺=右辺が成り立つので、
$$P_c \times \frac{L}{2} \theta = M_p 3 \theta$$
という仮想仕事式が完成しました。これで、崩壊荷重が求められました。
$$P_c = \frac{6 M_p}{L}$$
まとめ
お疲れ様でした。
崩壊荷重の問題は、崩壊機構の変形の図がきちんと描けるかどうかがポイントです。
図が描ければあとは変形図に合わせて仮想仕事式を立てて計算するだけです。最初はうまく描けなかったり、描いても右辺の$\Delta \theta$がうまく反映できなかったりします。でも、出題される問題はある程度テンプレ化しているので、覚えてしまえばスムーズに解けるようになるはずです。
以下、関連記事です。崩壊機構の図を描く参考にしてみてください。それでは、また。




































コメント