こんにちは、ゆるカピ(@yurucapi_san)です。
今回は座屈について解説していきたいと思います。
座屈とはどのような現象かイメージしてみましょう。細長い棒を押し込むと、地面に深く突き刺さる前に湾曲して変形します。逆に太くて短いものを押し込んでも、地面にめり込むだけで湾曲するような変形はしません。
このような湾曲して変形する現象のことを、座屈と呼んでいます。
部材は圧縮力を受けると、断面積の大きさに比例して縮む変形をして、最終的に圧縮破壊します。しかし、長柱のような細長い部材は、圧縮破壊するだけの力が作用する前に座屈して急に壊れてしまいます。
座屈について理解し、簡単に座屈しないような設計の工夫を考えてみましょう。
オイラー座屈を知る

座屈といっても、実際にはさまざまな種類の座屈があります。構造分野では、曲げ座屈、横座屈、局部座屈について考えて設計しています。
このなかで座屈の基本といえるのが、オイラー座屈と呼ばれる曲げ座屈です。柱のように棒状の細長い部材の座屈のことです。
座屈は急激に部材の耐力が低下してしまうため危険な現象です。建築物を支える柱が圧縮で壊れる前に、座屈で壊れないように設計しないといけません。
座屈荷重の関係を理解する

部材が座屈する限界の荷重を座屈荷重といいます。この値を超えたら座屈するという限界値です。
これは、コップの容量みたいなものです。小さいコップは少しの水であふれてしまいますが、大きいコップは少しの水ではあふれません。
座屈荷重を大きくしておけば座屈しにくい部材にすることができます。
座屈荷重の公式
座屈荷重$P_{cr}$の公式は以下のとおりです。この式は単純梁の横から水平力$P$をかけ続けていった時のたわみ曲線の式から求められます。
$$P_{cr} = \frac{\pi^2 EI}{l_k^2}$$
$E$はヤング係数、$I$は弱軸方向の断面二次モーメント、$l_k$は座屈長さを表しています。この式から、座屈荷重は部材の曲げ剛性$EI$によって大きく変わることがわかります。
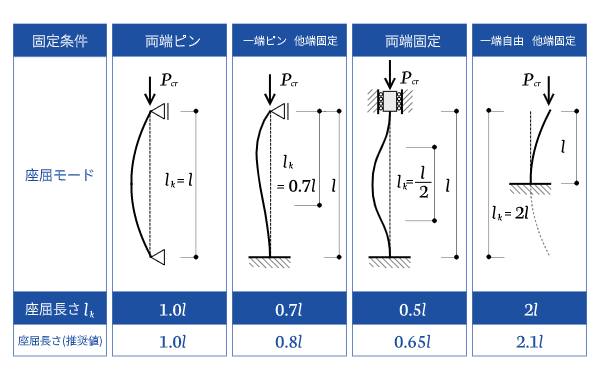
固定条件と座屈長さの関係
座屈長さ$l_k$は、部材の固定条件(境界条件)によって変わります。部材の長さ自体は変わりませんが、座屈に影響する有効長さが変わるということです。
細長い部材、例えば下敷きの端を手のひらで当てながら曲げた場合と、両端をしっかりとつかんだ状態で曲げた場合とで、湾曲の形状が違いますよね。
つまり、部材の端部の固定度が高くなると端部は曲げ変形しにくくなるので、座屈長さは短くなります。座屈長さが短くなると、座屈するまでに必要な力が大きくなるということです。
固定条件と座屈長さには次のような関係があります。
両端ピンを基準に考えると、両端固定にすると座屈長さは半分、片方が完全に自由な片持ち状態(例えば地面に突き刺さっている棒のようなイメージ)だと2倍の座屈長さになることがわかります。
座屈長さは座屈荷重の2乗に反比例なので、片持ちにすると両端ピンの場合の1/4の力で座屈してしまうことがわかります。
このインパクトは恐ろしいですね。固定条件を見直すだけで断面を大きくしなくて済む、ということも実際に起こり得ます。
座屈長さと細長比の関係を理解する
実際の設計では、直接座屈荷重を求めることはほとんどありません。軸力やせん断力、曲げモーメントと同じように、応力で評価するのが一般的です。
座屈荷重を応力に書き直すと以下のようになります。
$$\sigma_{cr} = \frac{P_{cr}}{A} = \frac{\pi^2 EI}{l_k^2 A} = \pi^2 E \frac{I}{l_k^2 A}$$
$\lambda = \frac{l_k}{i}$、$i = \sqrt{\frac{I}{A}}$とすると、
$$\sigma_{cr} = \frac{\pi^2 E}{\lambda^2}$$
となります。$\lambda$(ラムダ)のことを細長比、$i$を断面二次半径といいます。式から、細長比が小さいほうが座屈しにくいということがわかります。

細長比っていまいちよくわかんないんだよね〜。唐突に断面二次半径なんてのが出てくるから余計に理解が追いつかないよ。

確かに細長比って聞くと、部材の長さと断面積の関係かなって考えちゃうよね。でも、実際は座屈荷重でも触れたとおり、断面二次モーメントが深く影響しているんだよ。
このあたりは結構ややこしい話ですね。圧縮軸力の時は断面積が関係していましたが、座屈は曲げ変形なので断面二次モーメントが深く関係しているということになります。
断面二次半径については、断面積を基準とした時の断面二次モーメントの割合と考えることもできそうです。実際、同じ断面積でも、幅広の断面なのか、せいが大きく幅が狭い断面なのかによって座屈しやすさが左右されます。
断面二次半径の分母・分子どっちだったっけ、と迷った時の参考にしてみてください。もちろん、高校数学Ⅰ・Aになぞらえて覚えちゃってもいいですが•••。
座屈を防ぐには、断面二次半径のバランスが重要
最後に、部材の強軸、弱軸について触れておきたいと思います。
部材には方向によって曲がりやすさが違います。例えば、本の背表紙面を曲げるのは非常に大変ですが、表紙の麺を曲げるのは簡単です。
このように、部材を曲げにくい方向を強軸、曲げやすい方向を弱軸と呼んでいます。オイラー座屈は、少ない力で曲がる弱軸方向に対して発生します。部材のせいを大きくして幅を狭くしてしまうと、弱軸方向に座屈しやすくなります。
部材の幅とせいが同じくらいになると、強軸方向と弱軸方向の断面二次半径の差はかなり縮まります。部材の断面形状で座屈を防ごうと思ったら、なるべく幅広の断面にするといいでしょう。
実際、エレベーターの支柱や間柱でH形鋼を採用している場合は、部材の幅とせいが同じ幅広断面を使っていると思います。ガラス張りのエレベーターに乗る機会があったら、確認してみるといいかもしれません。

まとめ
お疲れ様でした。
今回は、オイラー座屈についてお伝えしました。現象そのものは身近な内容なのでわかりやすいのですが、座屈長さの固定条件と細長比のところでだいたい苦戦します。この部分は、符号と数字だけを丸暗記しても、おそらく理解はできないでしょう。
座屈長だや細長比については、一度自分で絵を描いてみるのがいいと思います。細長いプラスチックの定規を曲げてみるのも理解の助けになります。
以下、関連記事です。気になる人はこちらも合わせて読んでみると理解が深まると思います。それでは、また。


































コメント