こんにちは、ゆるカピ(@yurucapi_san)です。
あなたはトラスという言葉を聞いて、どんなイメージが浮かびますか?
トラス構造は、スタジアムや橋、工場などの大スパン構造でよく採用されている架構形式の1つです。子どもの頃、河川敷からトラス橋を眺めていて、スケールの大きさに圧倒されたのを憶えています。
建築関係者なら、構造と聞くとまず連想するのがトラスかもしれません。一級河川に架かっている橋はだいたいがトラス橋なので、身近に感じる人も多いでしょう。アーチ派の人がいたらすみません。
今回はそんなトラス構造について、どんな架構形式なのか、メリット、デメリットはどうなのかについて解説していきます。

計算問題を解く前にまずは基本を理解しよう。
どんな特徴があるのか

トラス構造には主に3つの特徴があります。この条件を満たしていたらトラス構造ともいえます。
- 部材同士を三角形につなぐ
- 直線材で両端がピン接合
- 部材の中間に外力、荷重が作用しない
あれ、これは実はトラス構造じゃないのか?というのがあるかもしれません。例えば、三角形の形状をしていればトラス構造と考えるかもしれませんが、構造力学ではそれだけではトラス構造になりません。あくまで部材の両端がピン接合になっていなければなりません。
ただし、実際には完全にピン接合のトラスを作ることはできないので、構造計算で考える理想化された力学モデルの話だと理解してください。
部材同士を三角形につなぐ
これはトラス構造の大前提といえる特徴です。
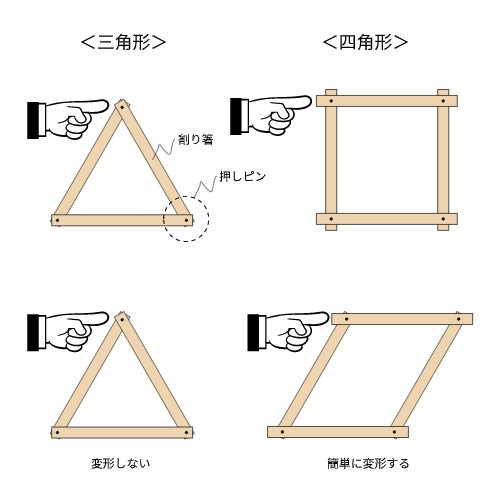
一般に、三角形で作られたものは四角形よりも変形しづらく強度が高いです。例えば、3本の割り箸で作った三角形のフレームと、4本の割り箸で作った四角形のフレームを考えてみましょう。フレームの隅は輪ゴムで留めるか、押しピンで固定されているとします。
これを手で押すと、四角形のほうは平行四辺形に簡単に変形しますが、三角形のほうはなかなか変形しません。四角形は割り箸の長さを保ったまま角度をつけて変形できますが、三角形は割り箸の長さが変わらない限り(割り箸が伸び縮みしない限り)変形できないからです。
この原理を架構に応用したのがトラス構造というわけです。
直線材で両端がピン接合
部材の両端をピン接合にすると曲げモーメントをゼロにすることができます。曲げモーメントがゼロなので、曲げに伴うせん断力もゼロになります。構造力学では部材の長さが極端に短いなどの例外を除いて、単独でせん断力は生じないとしています。
つまり、トラス構造には軸力しか生じないことがわかります。
部材の中間に外力、荷重が作用しない
意外と盲点ですが、部材の中間に力が作用すると部材そのものに曲げモーメントとせん断力が生じてしまいます。
トラス構造では、軸力のみが生じると考えているので、部材の中間には外力や荷重が作用しないと仮定して計算します。
このあたりはトラスの部材に自重があること、風荷重などは部材、節点関係なく一様に作用すると考えると、実際には当てはまらないでしょう。あくまで理想化された力学モデルだと割り切ったほうがいいと思います。
トラス構造のメリット・デメリット

トラス構造の特徴がわかったところで、設計するとなるとどんなメリット、デメリットがあるでしょうか。
ここで、メリット3つ、デメリット3つを挙げたいと思います。
- 部材断面を小さくできる
- たわみを抑えられる
- 空間をダイナミックに演出できる
- 施工の手間が大きい
- 斜材が目立つ
- 最低限必要なトラスせいがある
トラス構造のメリット
トラス構造のメリットは以下の3つです。
部材断面を小さくできる
トラス構造は軸力しか生じないので、部材断面を小さくすることができます。断面を小さく抑えることで構造材料のコストを下げることできます。
たわみを抑えられる
部材断面は小さくなる一方でトラスそのものを1つの梁部材と考えた時の梁せいは非常に大きいので、大スパンにすると出てくるたわみの問題を解消することができます。
たわみを抑えるためには断面二次モーメントを大きくする必要があります。断面二次モーメントとたわみの関係については以下の記事に書いてあるので確認してみてください。
長方形断面の断面二次モーメントの公式を思い出してください。梁幅$b$、梁せい$h$として、
$$I = \frac{bh^3}{12}$$
でした。この時、せい$h$が断面二次モーメントを大きくするのに効果的であることがわかると思います。同じ梁せいの断面よりも少ない部材量でたわみを抑えられるので、非常に経済的です。
空間をダイナミックに演出できる
空間をダイナミックに見せることができるのも、トラス構造のメリットの1つです。巨大な吹き抜け空間や跳ね出し空間を演出できるのもトラス構造の為せる業です。
トラス構造のデメリット
トラス構造のデメリットは3つあります。
施工の手間が大きい
トラス構造の一番のデメリットとして挙げられるのが施工コストが大きいことでしょう。トラス構造はその特性上、上弦材・下弦材(合わせて横材)、束材(縦材)、斜材の4種類の部材が必要になり、あらゆる角度から部材が取り付くため接合部が複雑になります。
施工コストが、材料コストを下げた分を相殺あるいは上回ってしまった、という逆転現象も起きてしまうことも実際あります。
斜材が目立つ
これはどちらかというと意匠的な問題です。最近は、鉄骨のブレース材をあえて見せるブルックリンスタイルが流行っていますが、施設計画上、あるいはデザイン上、制約が出てくるのは確かです。
最低限必要なトラスせいがある
トラスの斜材の角度が低すぎる(寝ているといいます)と、水平力に対する抵抗力の効きが悪くなってしまいます。逆に斜材の傾斜がきつくなると(立っているといいます)、こちらもトラス材としての効きが悪くなります。
つまり、トラスのスパン割とせいのバランスが良くないと、トラス構造の経済性が損なわれデメリットになってしまうということです。
さまざまな架構形状タイプ
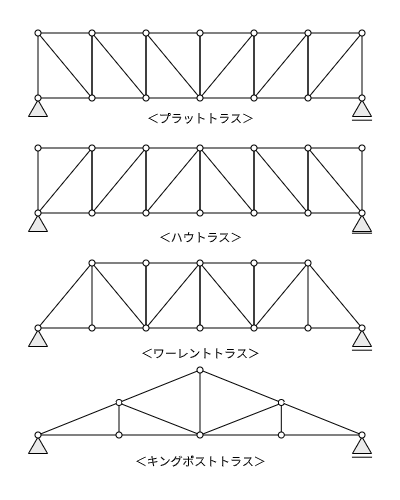
トラス構造は、その形状によってさまざまな名称が付けられています。
プラットトラスとハウトラスは斜材の向きがそれぞれ反対になっています。この2つの方式には、上から荷重がかかってきた時に斜材に引張力がかかるか、圧縮力がかかるかの違いがあります。
トラス構造の上弦材に載る重量物を支えるようにしたいのか、下弦材に載る重量物を上から吊るにしたいのかによって採用する方式が変わってきます。設計実務ではさまざまなパターンを試行錯誤しながら最終的な方式を決めていきます。
なお、鉄骨ブレースは通常、引張力のみを負担するように設計します。これは鋼材は座屈しやすく、圧縮力を十分に負担できないためです。
計算方法はなにがあるのか
トラス構造もラーメン構造と同じように、応力(軸力)の計算ができます。軸力を求める方法は2つあります。
- 節点法
- 切断法(断面法)
それぞれ計算に特徴がありますが、私のおすすめは切断法です。まずは、2つの計算方法の概要について説明します。
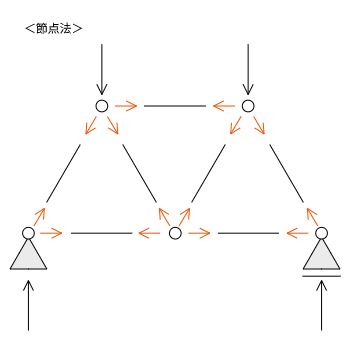
節点法
節点法は、節点にのみ外力や荷重が作用するというトラスの特徴に注目して、各節点での力のつり合い式から軸力を求めていく方法です。力のつり合い式も鉛直方向と水平方向だけを考えればよく、わかりやすいので構造力学に慣れていない人に向いている計算方法です。
ただし、支点反力や外力が作用している端からしか計算できないため、問題によっては求めたい軸力の計算にたどり着くまでに時間がかかってしまう可能性があります。
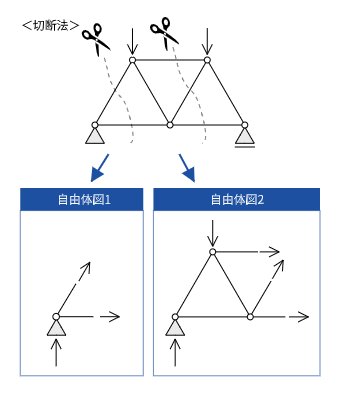
切断法(断面法)
切断法は、部材を任意の位置で仮想的に切断し、鉛直方向、水平方向、回転方向の力のつり合い式から軸力を求める方法です。
計算には少しコツと慣れが必要ですが、必要な軸力をピンポイントで求められるので、時間に制約のある建築士試験などでかなり役に立ちます。
建築士試験のためにトラス構造を勉強している人は、切断法をマスターすることをおすすめします。
まとめ
お疲れ様でした。
今回は設計者の視点から、メリット、デメリットを含めたトラス構造の特徴についてまとめてみました。これで、トラス構造のイメージはつかめたのではないでしょうか。
トラスの計算がうまくいかないという人は、一度こういう基本の話に立ち返ってみるのもおすすめです。自分がどんな構造の問題を解こうとしているんだというイメージがつけば、計算の苦手意識が少し和らぐと思います。
ぜひ、次は計算にもチャレンジしてみてください。
それでは、また。



































コメント